Contenu

• Pas
• Conseils

La fonction rationnelle a la forme y = N (x) / D (x), où N et D sont des polynômes. Pour tracer une telle fonction avec précision, vous avez besoin d'une bonne connaissance de l'algèbre, y compris des calculs différentiels. Considérez l'exemple suivant : oui = (2X - 6X + 5)/(4X + 2).

Pas

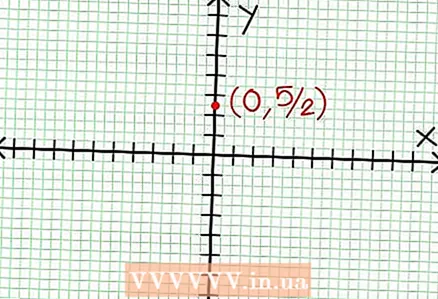1. 1 Trouvez l'ordonnée à l'origine du graphique. Pour ce faire, substituez x = 0 dans la fonction et obtenez y = 5/2. Ainsi, le point d'intersection du graphique avec l'axe Y a des coordonnées (0, 5/2).Placez ce point sur le plan de coordonnées.
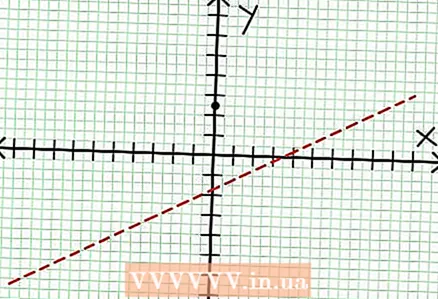2. 2 Trouvez les asymptotes horizontales. Divisez le numérateur par le dénominateur (dans une colonne) pour déterminer le comportement de "y" avec des valeurs de "x" tendant vers l'infini. Dans notre exemple, la division sera oui = (1/2)X - (7/4) + 17/(8X + 4). Pour les grandes valeurs positives ou négatives de "x" 17 / (8X + 4) tend vers zéro, et le graphique se rapproche de la droite donnée par la fonction oui = (1/2)X - (7/4). En utilisant la ligne pointillée, tracez cette fonction.
   • Si le degré du numérateur est inférieur au degré du dénominateur, alors vous ne pouvez pas diviser le numérateur par le dénominateur et l'asymptote sera décrite par la fonction à = 0.
   • Si le degré du numérateur est égal au degré du dénominateur, alors l'asymptote est une ligne horizontale égale au rapport des coefficients en "x" au degré le plus élevé.
   • Si le degré du numérateur est supérieur de 1 au degré du dénominateur, alors l'asymptote est une droite inclinée dont la pente est égale au rapport des coefficients en "x" au degré le plus élevé.
   • Si le degré du numérateur est supérieur au degré du dénominateur de 2, 3, etc., alors pour les grandes valeurs |N.-É.| sens à tendent vers l'infini (positif ou négatif) sous la forme d'un carré, cubique ou autre degré d'un polynôme. Dans ce cas, très probablement, vous n'avez pas besoin de construire un graphique exact de la fonction obtenue en divisant le numérateur par le dénominateur.
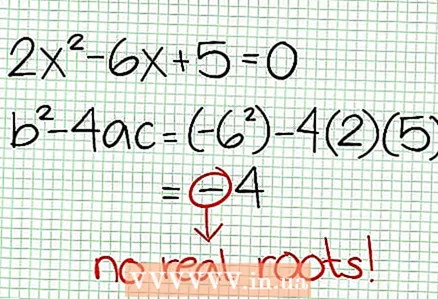3. 3 Trouvez les zéros de la fonction. Une fonction rationnelle a des zéros lorsque son numérateur est zéro, c'est-à-dire N (N.-É.) = 0. Dans notre exemple, 2X - 6X + 5 = 0. Le discriminant de cette équation quadratique : b - 4ca = 6 - 4 * 2 * 5 = 36 - 40 = -4. Puisque le discriminant est négatif, alors N (N.-É.), et donc F (N.-É.) n'a pas de racines réelles. Le graphique d'une fonction rationnelle ne coupe pas l'axe X. Si la fonction a des zéros (racines), placez-les sur le plan de coordonnées.
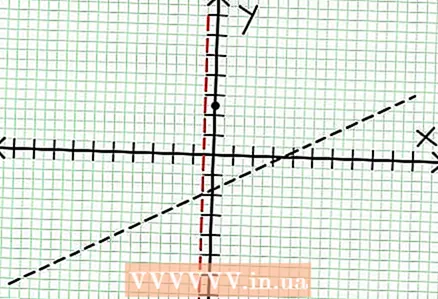4. 4 Trouvez les asymptotes verticales. Pour ce faire, mettez le dénominateur à zéro. Dans notre exemple, 4X + 2 = 0 et N.-É. = -1/2. Tracez l'asymptote verticale en utilisant la ligne pointillée. Si pour une valeur N.-É. N (N.-É.) = 0 et D (N.-É.) = 0, alors l'asymptote verticale existe ou n'existe pas (c'est un cas rare, mais il vaut mieux s'en souvenir).
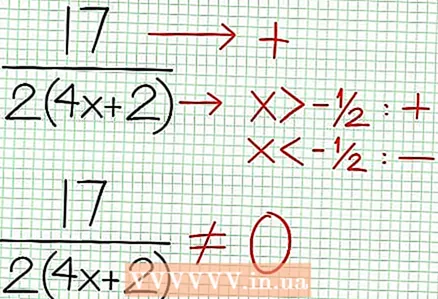5. 5 Regardez le reste du numérateur divisé par le dénominateur. Est-il positif, négatif ou nul ? Dans notre exemple, le reste est 17, ce qui est positif. Dénominateur 4X + 2 positif à droite de l'asymptote verticale et négatif à gauche de celle-ci. Cela signifie que le graphique de la fonction rationnelle pour les grandes valeurs positives N.-É. approche l'asymptote d'en haut, et pour les grandes valeurs négatives N.-É. - par le bas. Depuis 17 / (8X + 4) n'est jamais égal à zéro, alors le graphique de cette fonction ne coupera jamais la droite spécifiée par la fonction à = (1/2)N.-É. - (7/4).
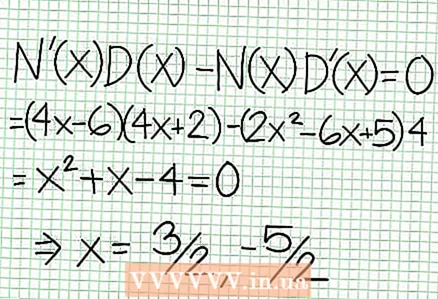6. 6 Trouvez les extrema locaux. Il existe un extremum local pour N'(X) RÉ (X) - N (X) RÉ '(X) = 0. Dans notre exemple, N '(X) = 4X - 6 et D' (X) = 4. N '(X) RÉ (X) - N (X) RÉ '(X) = (4X - 6)(4X + 2) - (2X - 6X + 5)*4 = X + X - 4 = 0. En résolvant cette équation, vous trouvez que X = 3/2 et X = -5/2. (Ce ne sont pas des valeurs tout à fait précises, mais elles conviennent à notre cas lorsque la superprécision n'est pas nécessaire.)
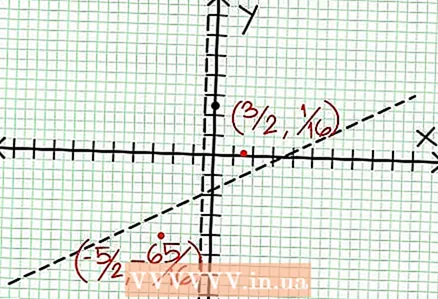7. 7 Trouver la valeur à pour chaque extremum local. Pour ce faire, remplacez les valeurs N.-É. dans la fonction rationnelle originelle. Dans notre exemple, f (3/2) = 1/16 et f (-5/2) = -65/16. Mettez de côté les points (3/2, 1/16) et (-5/2, -65/16) sur le plan de coordonnées. Étant donné que les calculs sont basés sur des valeurs approximatives (de l'étape précédente), le minimum et le maximum trouvés ne sont pas non plus tout à fait exacts (mais probablement très proches des valeurs exactes). (Le point (3/2, 1/16) est très proche du minimum local. A partir de l'étape 3, on sait que à toujours positif pour N.-É.> -1/2, et nous avons trouvé une petite valeur (1/16) ; ainsi, la valeur d'erreur est extrêmement faible dans ce cas.)
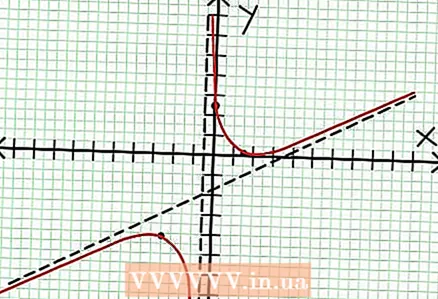8. 8 Connectez les points en attente et étendez doucement le graphique jusqu'aux asymptotes (n'oubliez pas la direction correcte du graphique approchant les asymptotes). N'oubliez pas que le graphique ne doit pas croiser l'axe des X (voir étape 3). Le graphique n'intersecte pas non plus les asymptotes horizontale et verticale (voir étape 5). Ne changez pas la direction du graphique sauf aux points extrêmes trouvés à l'étape précédente.

Conseils

• Si vous avez suivi les étapes ci-dessus strictement dans l'ordre, alors il n'est pas nécessaire de calculer les dérivées secondes (ou des quantités complexes similaires) pour tester votre solution.
• Si vous n'avez pas besoin de calculer les valeurs des quantités, vous pouvez remplacer la recherche d'extrema locaux par le calcul de quelques paires de coordonnées supplémentaires (N.-É., à) entre chaque paire d'asymptotes. De plus, si vous ne vous souciez pas du fonctionnement de la méthode décrite, ne soyez pas surpris de savoir pourquoi vous ne pouvez pas trouver la dérivée et résoudre l'équation N '(X) RÉ (X) - N (X) RÉ '(X) = 0.
• Dans certains cas, vous devrez travailler avec des polynômes d'ordre supérieur. Si vous ne pouvez pas trouver la solution exacte à l'aide de la factorisation, des formules, etc., estimez les solutions possibles à l'aide de méthodes numériques telles que la méthode de Newton.
• Dans de rares cas, le numérateur et le dénominateur partagent un facteur variable commun. Selon les étapes décrites, cela conduira à zéro et à une asymptote verticale au même endroit. Cependant, cela n'est pas possible, et l'explication est l'une des suivantes :
  • Zéro dans N (N.-É.) a une multiplicité plus élevée que zéro dans D (N.-É.). Graphique F (N.-É.) tend vers zéro à ce point, mais n'y est pas défini. Indiquez-le en dessinant un cercle autour du point.
  • Zéro dans N (N.-É.) et zéro dans D (N.-É.) ont la même multiplicité. Le graphique s'approche d'un point non nul à cette valeur N.-É.mais n'y est pas défini. Indiquez-le en dessinant un cercle autour du point.
  • Zéro dans N (N.-É.) a une multiplicité inférieure à zéro dans D (N.-É.). Il y a ici une asymptote verticale.