Contenu

• Pas
• Conseil

Si vous êtes mathématicien ou programmeur graphique, vous devrez probablement trouver l'angle entre deux vecteurs donnés. Dans cet article, wikiHow vous montre comment faire exactement cela.

Pas

Partie 1 sur 2: Trouvez l'angle entre deux vecteurs

1. 

   Définition de vecteur. Notez toutes les informations sur les deux vecteurs dont vous disposez. Supposons que vous ne disposiez que des paramètres spécifiés de leurs coordonnées dimensionnelles (également appelées composants). Si vous connaissez déjà la longueur (magnitude) d'un vecteur, vous pouvez ignorer certaines des étapes ci-dessous.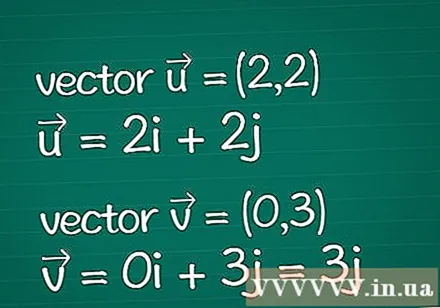
   • Exemple: vecteur bidimensionnel = (2,2) et vecteur bidimensionnel = (0,3). Ils peuvent également être écrits comme = 2je + 2j et = 0je + 3j = 3j.
   • Bien que des vecteurs bidimensionnels soient utilisés dans l'exemple de cet article, les instructions suivantes peuvent s'appliquer aux vecteurs avec n'importe quel nombre de dimensions.

2. 

   
   
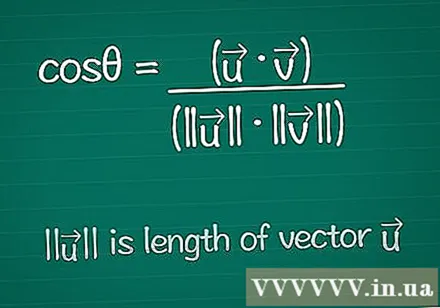
   Écrivez la formule cosinus. Pour trouver l'angle θ entre deux vecteurs, nous commençons par la formule pour trouver le cosinus pour cet angle. Vous pouvez en savoir plus sur cette formule ci-dessous, ou simplement l'écrire comme ceci:
   • cosθ = (•) / (|||| ||||)
   • |||| signifie "longueur du vecteur".
   • • est le produit scalaire des deux vecteurs - cela sera expliqué ci-dessous.

3. 

   
   
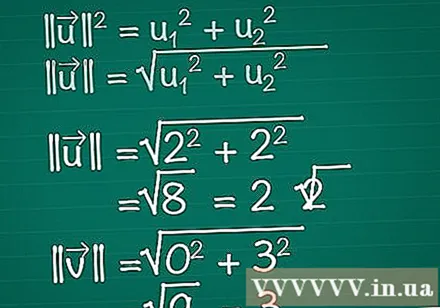
   Calculez la longueur de chaque vecteur. Imaginons qu'un triangle rectangle soit composé des composantes x, y du vecteur et du vecteur lui-même. Le vecteur forme l'hypoténuse du triangle, donc pour trouver sa longueur, nous utilisons le théorème de Pythagore. En fait, cette formule peut être facilement étendue à un vecteur de n'importe quel nombre de dimensions.
   • || u || = u₁ + u₂. Si un vecteur a plus de deux éléments, il vous suffit de continuer à ajouter + u₃ + u₄ +...
   • Par conséquent, pour un vecteur bidimensionnel, || u || = √ (u₁ + u₂).
   • Dans cet exemple, |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
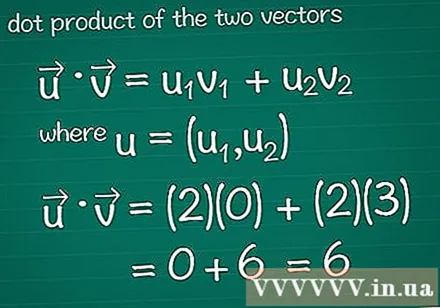
   Calculez le produit scalaire de deux vecteurs. Peut-être avez-vous appris la méthode de multiplication vectorielle, également connue sous le nom de scalaire cette. Pour calculer le produit scalaire par rapport à leur composition, multipliez les ingrédients dans chaque direction ensemble, puis additionnez le résultat entier.
   • Pour le programme graphique, veuillez vous reporter aux conseils avant de poursuivre la lecture.
   • En maths • = u₁v₁ + u₂v₂, où, u = (u₁, u₂). Si le vecteur a plus de deux éléments, ajoutez simplement + u₃v₃ + u₄v₄...
   • Dans cet exemple, • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. C'est le produit scalaire du vecteur et du vecteur.

5. 

   Mettez les résultats dans la formule. Rappelez-vous que cosθ = (•) / (|||| || ||). Nous connaissons maintenant à la fois le produit scalaire et la longueur de chaque vecteur. Entrez-les dans la formule pour calculer le cosinus de l'angle.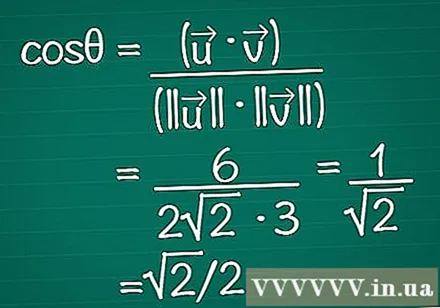
   • Dans notre exemple, cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Trouvez l'angle en fonction de son cosinus. Vous pouvez utiliser la fonction arccos ou cos dans une calculatrice pour trouver θ à partir d'une valeur cos connue. Avec certains résultats, vous pouvez trouver l'angle en fonction du cercle unitaire.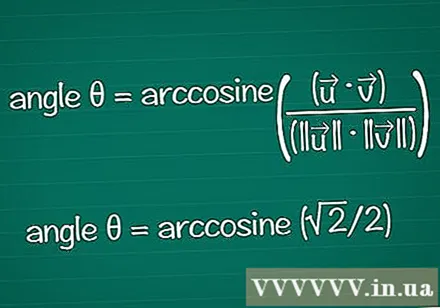
   • Dans l'exemple, cosθ = √2 / 2. Entrez "arccos (√2 ​​/ 2)" dans votre calculatrice pour trouver l'angle. Ou bien, vous pouvez trouver l'angle θ sur le cercle unité, à la position cosθ = √2 / 2. C'est vrai pour θ = /₄ ou 45º.
   • En combinant tout, la formule finale est: angle θ = arccosinus ((•) / (|||| || ||))
   publicité

Partie 2 sur 2: Détermination de la formule d'angle

1. 

   Comprenez le but de la formule. Cette formule n'est pas dérivée des règles existantes. Au lieu de cela, il est formé comme la définition du produit scalaire et de l'angle entre les deux vecteurs. Même ainsi, ce n'était pas une décision arbitraire. En revenant à la géométrie de base, nous pouvons comprendre pourquoi cette formule fournit des définitions intuitives et utiles.
   • Les exemples ci-dessous utilisent des vecteurs bidimensionnels car ils sont les plus faciles à comprendre et les plus simples. Les vecteurs tridimensionnels ou plus ont des propriétés définies par des formules générales presque similaires.

2. 

   Revoyez le théorème de Cosine. Considérons un triangle ordinaire avec un angle θ entre les côtés a et b, côté opposé c. Le théorème du cosinus stipule que c = a + b -2abcos(θ). Ce résultat est tiré tout simplement de la géométrie de base.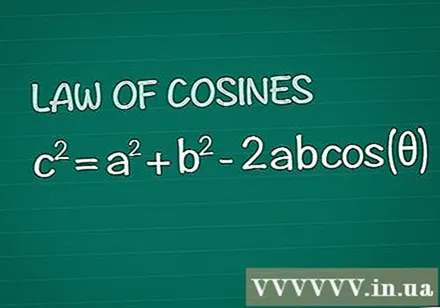

3. 

   Connectez deux vecteurs, formant un triangle. Dessinez une paire de vecteurs bidimensionnels sur papier, vecteurs et vecteurs, avec θ étant l'angle entre eux. Dessinez un troisième vecteur entre ces deux pour créer un triangle. En d'autres termes, dessinez un vecteur tel que + =. Vecteur = -.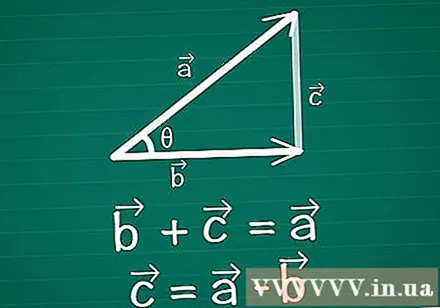

4. 

   Écris le théorème du cosinus pour ce triangle. Remplacez la longueur de côté de notre "triangle vectoriel" par le théorème du cosinus:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||cos(θ)

5. 

   Réécrire avec un produit scalaire. N'oubliez pas qu'un produit scalaire est l'image d'un vecteur sur l'autre. Le produit scalaire d'un vecteur avec lui-même ne nécessite aucune projection, car ici, il n'y a pas de différence de direction. Cela signifie • = || a ||. En utilisant cela, nous réécrivons l'équation:
   • (-) • (-) = • + • - 2 || a || || b ||cos(θ)

6. 

   Réécriture réussie de la même formule. Développez le côté gauche de la formule, puis simplifiez pour obtenir la formule utilisée pour trouver les angles.
   • • - • - • + • = • + • - 2 || a || || b ||cos(θ)
   • - • - • = -2 || a || || b ||cos(θ)
   • -2 (•) = -2 || a || || b ||cos(θ)
   • • = || a || || b ||cos(θ)
   publicité

Conseil

• Pour changer les valeurs et résoudre le problème rapidement, utilisez cette formule pour n'importe quelle paire de vecteurs bidimensionnels: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Si vous travaillez avec un logiciel d'infographie, vous n'aurez probablement à vous soucier que des dimensions du vecteur et non de sa longueur. Suivez les étapes suivantes pour raccourcir une équation et accélérer votre programme:
  • Normaliser chaque vecteur pour qu'il soit 1. Pour ce faire, divisez chacune des composantes du vecteur par sa longueur.
  • Obtenez le produit normalisé du scalaire au lieu du vecteur d'origine.
  • Puisque la longueur est 1, nous pouvons exclure les éléments de longueur de l'équation. Enfin, l'équation angulaire obtenue est arccos (•).
• Sur la base de la formule cosinus, nous pouvons déterminer rapidement si l'angle est aigu ou obtus. Commencez par cosθ = (•) / (|||| ||||):
  • Les côtés gauche et droit de l'équation doivent avoir le même signe (positif ou négatif).
  • Puisque la longueur est toujours positive, cosθ doit avoir le même signe que le produit scalaire.
  • Par conséquent, si le produit est positif, cosθ est également positif. Nous sommes dans le premier quadrant du cercle unité, avec θ <π / 2 ou 90º. L'angle à trouver est l'angle aigu.
  • Si le produit scalaire est négatif, cosθ est négatif. Nous sommes dans le deuxième quadrant du cercle unité, avec π / 2 <θ ≤ π ou 90º <θ ≤ 180º. C'est le coin de la prison.