Contenu

• Pas
• Conseil

Contrairement à une ligne droite, le coefficient de pente (pente) change constamment à mesure qu'il se déplace le long de la courbe. Le calcul donne l'idée que chaque point du graphique peut être exprimé sous la forme d'un coefficient d'angle ou de «taux de changement instantané». La ligne tangente en un point est une ligne qui a le même coefficient angulaire et passe par le même point. Pour trouver une équation de ligne tangente, vous devez savoir comment dériver l'équation d'origine.

Pas

Méthode 1 sur 2: Trouvez l'équation de la ligne tangente

1. 

   Fonctions graphiques et lignes tangentes (cette étape est facultative, mais recommandée). Le tableau vous aidera à comprendre plus facilement le problème et à vérifier si la réponse est raisonnable ou non. Dessinez des graphiques de fonction sur du papier quadrillé, utilisez la calculatrice scientifique avec la fonction graphique pour référence si nécessaire. Tracez une ligne tangente passant par un point donné (rappelez-vous que la ligne tangente passe par ce point et a la même pente que le graphique).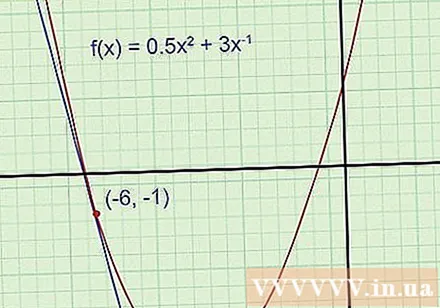
   • Exemple 1: Dessin parabolique. Tracez une ligne tangente passant par le point (-6, -1).
     Même si vous ne connaissez pas l'équation tangente, vous pouvez toujours voir que sa pente est négative et que l'ordonnée est négative (bien en dessous du sommet parabolique avec l'ordonnée de -5,5). Si la réponse finale trouvée ne correspond pas à ces détails, il doit y avoir une erreur dans votre calcul et vous devez vérifier à nouveau.

2. 

   
   
   Obtenez la première dérivée pour trouver l'équation pente de la ligne tangente. Avec la fonction f (x), la première dérivée f '(x) représente l'équation de la pente de la tangente en tout point de f (x). Il existe de nombreuses façons de prendre des dérivés. Voici un exemple simple utilisant la règle de puissance:
   • Exemple 1 (suite): Le graphe est donné par une fonction.
     Rappel de la règle de puissance lors de la prise de dérivée:.
     La première dérivée de la fonction = f '(x) = (2) (0,5) x + 3 - 0.
     f '(x) = x + 3. En remplaçant x par une valeur quelconque a, l'équation nous donnera la pente de la fonction tangente f (x) au point x = a.

3. 

   
   
   Entrez la valeur x du point considéré. Lisez le problème pour trouver les coordonnées du point pour trouver la ligne tangente. Entrez la coordonnée de ce point en f '(x). Le résultat obtenu est la pente de la ligne tangente au point ci-dessus.
   • Exemple 1 (suite): Le point mentionné dans l'article est (-6, -1). En utilisant une tension diagonale -6 dans f '(x):
     f '(- 6) = -6 + 3 = -3
     La pente de la tangente est -3.

4. 

   
   
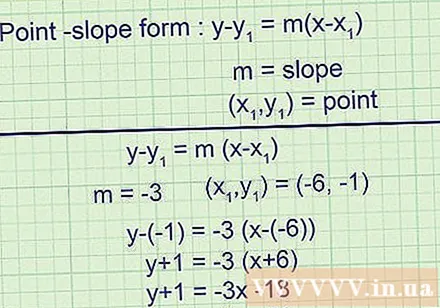
   Ecrivez une équation pour une tangente avec la forme d'une droite connaissant le coefficient de l'angle et un point dessus. Cette équation linéaire s'écrit. À l'intérieur, m est la pente et est un point sur la ligne tangente. Vous avez maintenant toutes les informations nécessaires pour écrire une équation tangente sous cette forme.
   • Exemple 1 (suite):
     La pente de la tangente est -3, donc:
     La ligne tangente passe par le point (-6, -1), donc l'équation finale est:
     Bref, nous pouvons:
     

5. 

   Confirmation graphique. Si vous avez une calculatrice graphique, tracez la fonction d'origine et la ligne tangente pour vérifier si la réponse est correcte. Si vous faites des calculs sur papier, utilisez des graphiques dessinés plus tôt pour vous assurer qu'il n'y a pas d'erreurs évidentes dans votre réponse.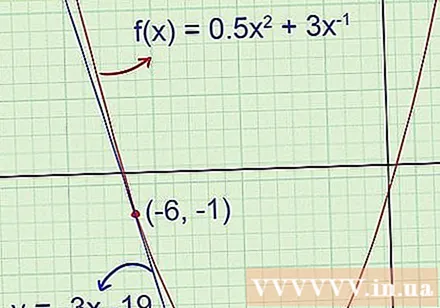
   • Exemple 1 (suite): Le dessin initial montre que la ligne tangente a des coefficients d'angle négatifs et que le décalage est bien inférieur à -5,5. L'équation tangente que nous venons de trouver est y = -3x -19, ce qui signifie que -3 est la pente de l'angle et -19 est l'ordonnée.

6. 

   Essayez de résoudre un problème plus difficile. Nous reprenons toutes les étapes ci-dessus.À ce stade, le but est de trouver la ligne tangente de at x = 2: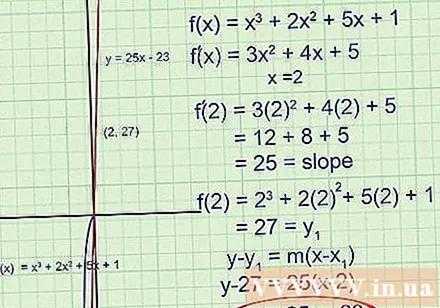
   • Trouvez le premier dérivé en utilisant la règle de puissance:. Cette fonction nous donnera la pente de la tangente.
   • Pour x = 2, recherchez. C'est la pente à x = 2.
   • Notez que cette fois, nous n'avons pas de point et seulement la coordonnée x. Pour trouver la coordonnée y, remplacez x = 2 dans la fonction d'origine:. Le score est de (2,27).
   • Écrivez une équation pour une ligne tangente passant par un point et ayant le coefficient de l'angle déterminé:
     
     Si nécessaire, réduisez à y = 25x - 23.
   publicité

Méthode 2 sur 2: Résoudre les problèmes connexes

1. 

   Trouvez l'extrême sur le graphique. Ce sont les points auxquels le graphe se rapproche d'un maximum local (un point supérieur aux points voisins des deux côtés) ou d'un minimum local (inférieur aux points voisins des deux côtés). La ligne tangente a toujours un coefficient nul en ces points (une ligne horizontale). Cependant, le coefficient de l'angle ne suffit pas pour conclure que c'est le point extrême. Voici comment les trouver: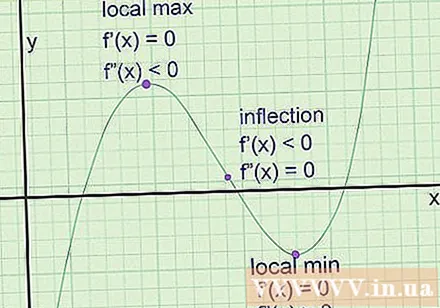
   • Prenez la première dérivée de la fonction pour obtenir f '(x), la pente de la pente de la tangente.
   • Résolvez l'équation f '(x) = 0 pour trouver le point extrême potentiel.
   • En prenant la dérivée quadratique pour obtenir f '(x), l'équation nous indique le taux de changement de la pente de la tangente.
   • À chaque extrême potentiel, changez la coordonnée une en f '' (x). Si f '(a) est positif, nous avons un minimum local à une. Si f '(a) est négatif, nous avons un maximum local. Si f '(a) vaut 0, ce ne sera pas l'extrême, mais un point d'inflexion.
   • Si max ou min atteint à une, trouvez f (a) pour déterminer l'intersection.

2. 

   Trouvez les équations de la normale. La ligne "normale" d'une courbe au point a passera par ce point et perpendiculairement à la ligne tangente. Pour trouver l'équation de la normale, utilisez ce qui suit: (pente de la normale) (pente de la normale) = -1 lorsqu'ils passent le même point sur le graphique. Plus précisément: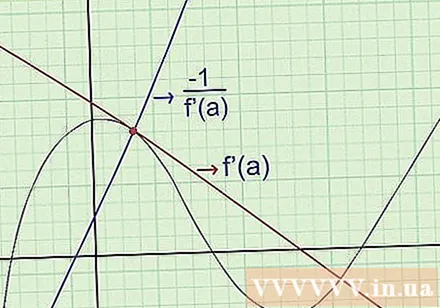
   • Trouvez f '(x), la pente de la tangente.
   • Si en un point donné, on a x = une: trouvez f '(a) pour déterminer la pente en ce point.
   • Calculez pour trouver le coefficient de la normale.
   • Écrivez l'équation de la perpendiculaire pour connaître les coefficients de l'angle et d'un point par lequel elle passe.
   publicité

Conseil

• Si nécessaire, réécrivez l'équation d'origine sous forme standard: f (x) = ... ou y = ...