Contenu

• Pas
• Conseil

La variance mesure la dispersion de l'ensemble de données. Il est très utile pour créer des modèles statistiques: une faible variance peut indiquer que vous décrivez une erreur aléatoire ou du bruit au lieu de la relation sous-jacente dans les données. Avec cet article, wikiHow vous apprend à calculer la variance.

Pas

Méthode 1 sur 2: Calculer la variance d'un échantillon

1. 

   Écrivez votre exemple d'ensemble de données. Dans la plupart des cas, les statisticiens ne disposent d'informations que sur un échantillon ou un sous-ensemble de la population qu'ils étudient. Par exemple, au lieu de faire une analyse générale du «coût de toutes les voitures en Allemagne», un statisticien pourrait trouver le coût d'un échantillon aléatoire de quelques milliers de voitures. Le statisticien peut utiliser cet échantillon pour obtenir une bonne estimation du coût des voitures en Allemagne. Cependant, il est plus probable qu'il ne correspondra pas exactement aux chiffres réels.
   • Par exemple: Lors de l'analyse du nombre de muffins vendus par jour dans un café, vous avez prélevé un échantillon aléatoire de six jours et obtenu les résultats suivants: 38, 37, 36, 28, 18, 14, 12, 11, 10,7, 9,9. Il s'agit d'un échantillon, pas d'une population, car vous ne disposez pas de données pour chaque jour d'ouverture du magasin.
   • Si chaque Points de données dans le maître, veuillez passer à la méthode ci-dessous.

2. 

   
   
   Notez l'exemple de formule de variance. La variance d'un ensemble de données indique le degré de dispersion des points de données. Plus la variance est proche de zéro, plus les points de données sont regroupés. Lorsque vous utilisez des exemples d'ensembles de données, utilisez la formule suivante pour calculer la variance:
   • = /_{(n - 1)}
   • est la variance. La variance est toujours calculée en unités au carré.
   • représente une valeur dans votre ensemble de données.
   • ∑, qui signifie «somme», vous indique de calculer les paramètres suivants pour chaque valeur, puis de les additionner.
   • x̅ est la moyenne de l'échantillon.
   • n est le nombre de points de données.

3. 

   
   
   Calculer la moyenne de l'échantillon. Le symbole x̅ ou "x-horizontal" est utilisé pour indiquer la moyenne de l'échantillon. Calculez comme vous le feriez pour n'importe quelle moyenne: additionnez tous les points de données et divisez-les par le nombre de points.
   • Par exemple: Tout d'abord, additionnez vos points de données: 17 + 15 + 23 + 7 + 9 + 13 = 84
     Ensuite, divisez le résultat par le nombre de points de données, dans ce cas six: 84 ÷ 6 = 14.
     Moyenne de l'échantillon = x̅ = 14.
   • Vous pouvez considérer la moyenne comme le "point central" des données. Si les données sont centrées autour de la moyenne, la variance est faible. S'ils sont dispersés loin de la moyenne, la variance est élevée.

4. 

   
   
   Soustrayez la moyenne de chaque point de données. Il est maintenant temps de calculer - x̅, où se trouve chaque point de votre ensemble de données. Chaque résultat indiquera un écart par rapport à la moyenne de chaque point correspondant, ou pour le dire simplement, la distance qui le sépare de la moyenne.
   • Par exemple:
     - x̅ = 17 - 14 = 3
     - x̅ = 15 - 14 = 1
     - x̅ = 23 - 14 = 9
     - x̅ = 7 - 14 = -7
     - x̅ = 9 - 14 = -5
     - x̅ = 13 - 14 = -1
   • Il est très facile de vérifier vos calculs, car les résultats doivent totaliser zéro, car par la moyenne, les résultats négatifs (la distance de la moyenne aux petits nombres). les résultats positifs (distance entre la moyenne et les plus grands nombres) sont complètement éliminés.

5. 

   Mettez tous les résultats au carré. Comme indiqué ci-dessus, la liste d'écarts courante (- x̅) a une somme de zéro, ce qui signifie que «l'écart moyen» sera toujours égal à zéro et que rien ne peut être dit sur la dispersion des données. Pour résoudre ce problème, nous trouvons le carré de chaque écart. Grâce à cela, tous sont des nombres positifs, les valeurs négatives et les valeurs positives ne s'annulent plus et donnent la somme zéro.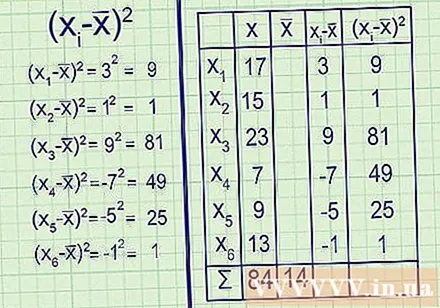
   • Par exemple:
     (- X)
     - X)
     9 = 81
     (-7) = 49
     (-5) = 25
     (-1) = 1
   • Vous avez maintenant (- x̅) pour chaque point de données de l'échantillon.

6. 

   Trouvez la somme des valeurs au carré. Il est maintenant temps de calculer le numérateur entier de la formule: ∑. Le grand cyclo, ∑, nécessite que vous ajoutiez la valeur d'élément suivante pour chaque valeur. Vous avez calculé (- x̅) pour chaque valeur de l'échantillon, il ne vous reste donc qu'à additionner les résultats.
   • Par exemple: 9 + 1 + 81 + 49 + 25 + 1 = 166.

7. 

   Divisez par n - 1, où n est le nombre de points de données. Il y a longtemps, lors du calcul de la variance de l'échantillon, les statisticiens ne divisaient que par n. Cette division vous donnera la moyenne de l'écart au carré, qui correspond exactement à la variance de cet échantillon. Cependant, gardez à l'esprit que l'échantillon n'est qu'une estimation d'une population plus large. Si vous prenez un autre échantillon aléatoire et faites le même calcul, vous obtiendrez un résultat différent. En fait, diviser par n-1 au lieu de n vous donne une meilleure estimation de la variance d'une population plus large - ce qui vous tient vraiment à cœur. Cette correction est si courante qu'elle constitue désormais la définition acceptée de la variance de l'échantillon.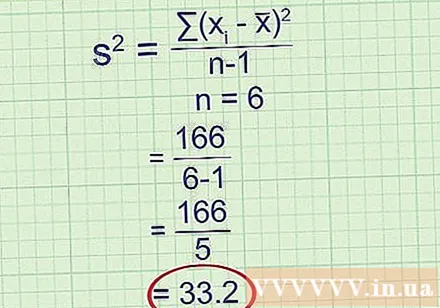
   • Par exemple: Il y a six points de données dans l'échantillon, donc n = 6.
     Échantillon de variance = 33,2

8. 

   Comprenez la variance et l'écart type. Notez que, puisqu'il y a des puissances dans la formule, la variance est mesurée dans le carré des unités des données d'origine. Ceci est visuellement déroutant. Au lieu de cela, l'écart type est souvent très utile. Mais il ne sert à rien de gaspiller des efforts, car l'écart type est déterminé par la racine carrée de la variance. C'est pourquoi la variance de l'échantillon est écrite en termes, et l'écart type d'un échantillon l'est.
   • Par exemple, l'écart type de l'échantillon ci-dessus = s = √33,2 = 5,76.
   publicité

Méthode 2 sur 2: Calculer la variance d'une population

1. 

   En commençant par l'ensemble de données de base. Le terme «population» est utilisé pour désigner toutes les observations pertinentes. Par exemple, si vous recherchez l'âge des résidents de Hanoi, votre population globale comprendra l'âge de toutes les personnes vivant à Hanoi. Habituellement, vous créez une feuille de calcul pour un grand ensemble de données comme celui-ci, mais voici un exemple d'ensemble de données plus petit:
   • Par exemple: Dans la salle d'un aquarium, il y a exactement six aquariums. Ces six réservoirs contiennent les nombres de poissons suivants:
     
     
     
     
     
     

2. 

   Notez la formule de la variance globale. Puisqu'une population contient toutes les données dont nous avons besoin, cette formule nous donne la variance exacte de la population. Pour le distinguer de la variance de l'échantillon (qui n'est qu'une estimation), les statisticiens utilisent d'autres variables:
   • σ = /_n
   • σ = variance de l'échantillon. C'est la saucisse normalement carrée. La variance est mesurée en unités au carré.
   • représente un élément de votre ensemble de données.
   • L'élément en ∑ est calculé pour chaque valeur, puis additionné.
   • μ est la moyenne globale.
   • n est le nombre de points de données dans la population.

3. 

   Trouvez la moyenne de la population. Lors de l'analyse d'une population, le symbole μ ("mu") représente la moyenne arithmétique. Pour trouver la moyenne, additionnez tous les points de données, puis divisez par le nombre de points.
   • Vous pouvez considérer la moyenne comme «moyenne», mais soyez prudent, car le mot a de nombreuses définitions mathématiques.
   • Par exemple: valeur moyenne = μ = = 10,5

4. 

   Soustrayez la moyenne de chaque point de données. Les points de données plus proches de la moyenne ont une différence plus proche de zéro. Répétez le problème de soustraction pour tous les points de données et vous commencerez probablement à ressentir la dispersion des données.
   • Par exemple:
     - μ = 5 – 10,5 = -5,5
     - μ = 5 – 10,5 = -5,5
     - μ = 8 – 10,5 = -2,5
     - μ = 12 - 10., = 1,5
     - μ = 15 – 10,5 = 4,5
     - μ = 18 – 10,5 = 7,5

5. 

   Mettez chaque signe au carré. À ce stade, certains résultats obtenus à l'étape précédente seront négatifs et certains seront positifs.Si vous visualisez les données sur une ligne isomorphe, ces deux éléments représentent les nombres à gauche et à droite de la moyenne. Cela ne serait d'aucune utilité pour le calcul de la variance, car ces deux groupes s'annuleraient mutuellement. Au lieu de cela, placez-les tous pour qu'ils soient tous positifs.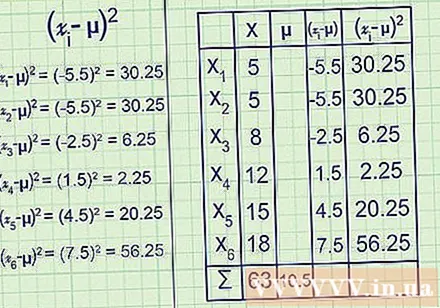
   • Par exemple:
     (- μ) pour chaque valeur de je va de 1 à 6:
     (-5,5) = 30,25
     (-5,5) = 30,25
     (-2,5) = 6,25
     (1,5) = 2,25
     (4,5) = 20,25
     (7,5) = 56,25

6. 

   Trouvez la moyenne de vos résultats. Vous avez maintenant une valeur pour chaque point de données, liée (pas directement) à la distance entre ce point de données et la moyenne. Faites la moyenne en les additionnant et en divisant par le nombre de valeurs que vous avez.
   • Par exemple:
     Variance globale = 24,25

7. 

   Recette de contact. Si vous n'êtes pas sûr de savoir comment cela correspond à la formule décrite au début de la méthode, notez tout le problème à la main et n'abréviez pas: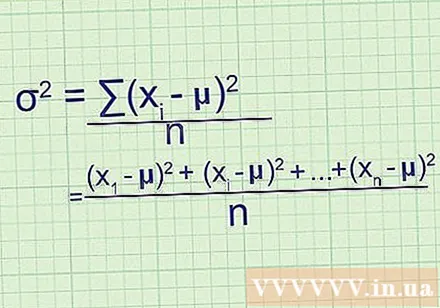
   • Après avoir trouvé la différence entre la moyenne et la quadrature, vous obtenez (- μ), (- μ), et ainsi de suite jusqu'à (- μ), où est le dernier point de données. dans l'ensemble de données.
   • Pour trouver la moyenne de ces valeurs, additionnez-les et divisez par n: ((- μ) + (- μ) + ... + (- μ)) / n
   • Après avoir réécrit le numérateur avec la notation sigmoïde, vous avez /_n, variance de formule.
   publicité

Conseil

• Comme la variance est difficile à interpréter, cette valeur est souvent calculée comme point de départ pour trouver l'écart type.
• Utiliser "n-1" au lieu de "n" dans le dénominateur est une technique appelée correction de Bessel. L'échantillon n'est qu'une estimation d'une population complète et la moyenne de l'échantillon présente un certain biais pour correspondre à cette estimation. Cette correction élimine le biais ci-dessus. Cela concerne le fait qu'une fois que n - 1 points de données ont été énumérés, le dernier point n était une constante, car seules certaines valeurs ont été utilisées pour calculer la moyenne de l'échantillon (x̅) dans la formule de variance.