Contenu

• Pas
• Méthode 1 sur 3: Comprendre l'énoncé du problème
• Méthode 2 sur 3: Formuler la preuve
• Méthode 3 sur 3: Notez les preuves
• Conseils

Trouver une preuve mathématique peut être une tâche intimidante, mais connaître les mathématiques et rédiger la preuve vous aidera. Malheureusement, il n'existe pas de méthodes simples et rapides pour apprendre à résoudre des problèmes mathématiques. Il est nécessaire d'étudier correctement le sujet et de se souvenir des théorèmes et définitions de base qui vous seront utiles pour prouver un postulat mathématique particulier. Étudiez des exemples de preuves mathématiques et entraînez-vous pour vous aider à améliorer vos compétences.

Pas

Méthode 1 sur 3: Comprendre l'énoncé du problème

1. 1 Déterminez ce que vous voulez trouver. La première étape consiste à déterminer ce qui doit être prouvé exactement. Entre autres choses, cela déterminera la dernière déclaration de votre preuve. À ce stade, vous devez également faire certaines hypothèses dans lesquelles vous travaillerez. Pour mieux comprendre le problème et commencer à le résoudre, découvrez ce que vous devez prouver et faites les hypothèses nécessaires.
2. 2 Dessinez un dessin. Lors de la résolution de problèmes mathématiques, il est parfois utile de les représenter sous la forme d'une image ou d'un diagramme. Ceci est particulièrement important dans le cas de problèmes géométriques - le dessin aide à visualiser l'état et facilite grandement la recherche d'une solution.
   • Lors de la création d'une image ou d'un diagramme, utilisez les données fournies dans la condition. Marquez les quantités connues et inconnues sur la figure.
   • Le dessin vous permettra de trouver plus facilement les preuves.
3. 3 Etudier des preuves de théorèmes similaires. Si vous ne pouvez pas trouver une solution tout de suite, trouvez des théorèmes similaires et voyez comment ils sont prouvés.
   • Notez que vous devez justifier chaque étape de la preuve. Voyez comment divers théorèmes sont prouvés sur Internet ou dans des manuels de mathématiques.
4. 4 Poser des questions. Ce n'est pas grave si vous n'arrivez pas à trouver des preuves tout de suite.Si vous n'êtes pas clair sur quelque chose, demandez à votre professeur ou à vos camarades de classe à ce sujet. Peut-être que vos camarades ont les mêmes questions et vous pouvez les trier ensemble. Il vaut mieux poser quelques questions que d'essayer de trouver des preuves encore et encore sans succès.
   • Allez voir le professeur après les cours et découvrez toutes les questions qui ne sont pas claires.

Méthode 2 sur 3: Formuler la preuve

1. 1 Formuler une preuve mathématique. Une preuve mathématique est une séquence d'énoncés soutenus par des théorèmes et des définitions qui prouvent un postulat mathématique. Les preuves sont le seul moyen de déterminer si un énoncé est mathématiquement correct.
   • La capacité à rédiger des preuves mathématiques témoigne d'une compréhension approfondie du problème et de la maîtrise des outils nécessaires (lemmes, théorèmes et définitions).
   • Une preuve rigoureuse peut vous aider à jeter un regard neuf sur les mathématiques et à ressentir leur fascination. Essayez simplement de prouver un énoncé pour vous faire une idée des méthodes mathématiques.
2. 2 Pensez à votre public. Avant de commencer à enregistrer des preuves, vous devez réfléchir à qui elles sont destinées et prendre en compte le niveau de connaissance de ces personnes. Si vous écrivez des preuves pour une publication ultérieure dans une revue scientifique, ce sera différent de lorsque vous faites un devoir scolaire.
   • Connaître votre public cible vous permettra d'écrire les preuves tout en formant vos lecteurs à les comprendre.
3. 3 Déterminer le type de preuve. Il existe plusieurs types de preuves mathématiques, et le choix d'une forme spécifique dépend du public cible et du problème à résoudre. Si vous ne savez pas quelle espèce choisir, vérifiez auprès de votre professeur. Au lycée, un justificatif à deux colonnes est exigé.
   • Lors de la rédaction des preuves en deux colonnes, l'une enregistre les données et les déclarations initiales et la seconde - la preuve correspondante de ces déclarations. Cette forme de notation est souvent utilisée lors de la résolution de problèmes géométriques.
   • Dans une manière moins formelle d'écrire des preuves, des constructions grammaticalement correctes et moins de symboles sont utilisés. Aux niveaux supérieurs, c'est la notation qui doit être utilisée.
4. 4 Esquissez la preuve en deux colonnes. Ce formulaire aide à organiser les pensées et à résoudre le problème de manière cohérente. Divisez la page en deux avec une ligne verticale et écrivez vos données d'origine et les déclarations qui en découlent sur le côté gauche. Écrivez les définitions et les théorèmes correspondants à droite de chaque énoncé.
   • Par exemple:
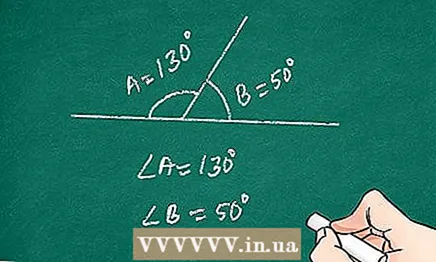
   • les coins A et B sont adjacents - donnés;
   • l'angle ABC est aplati - définit un coin aplati ;
   • l'angle ABC est de 180 ° - définissant une ligne droite;
   • angle A + angle B = angle ABC - la règle pour additionner les angles;
   • angle A + angle B = 180 ° - substitution;
   • l'angle A est complémentaire de l'angle B - définition d'angles supplémentaires ;
   • C.Q.D.
5. 5 Écrivez la preuve à deux colonnes comme une preuve informelle. Utilisez une entrée à deux colonnes comme base et écrivez la preuve sous une forme plus courte avec moins de symboles et d'abréviations.
   • Par exemple : supposons que les coins A et B soient adjacents. Selon l'hypothèse, ces angles se complètent. Lorsqu'ils sont adjacents, l'angle A et l'angle B forment une ligne droite. Si les côtés du coin forment une ligne droite, l'angle est de 180°. Additionnez les angles A et B pour créer une droite ABC. Ainsi, la somme des angles A et B est de 180°, c'est-à-dire que ces angles sont complémentaires. C.Q.D.

Méthode 3 sur 3: Notez les preuves

1. 1 Apprenez le langage de la preuve. Des déclarations et des phrases standard sont utilisées pour écrire des preuves mathématiques. Vous devez apprendre ces phrases et savoir les utiliser.
   • L'expression « Si A, alors B » signifie que si la déclaration A est vraie, alors la déclaration B doit également être vraie.
   • « A si et seulement si B » signifie que les déclarations A et B sont vraies ou fausses en même temps. Cette construction équivaut à deux énoncés simultanés : "Si A, alors B" et "Si A échoue, alors B ne tient pas".
   • « A seulement si B » est équivalent à « Si B, alors A », donc cette construction n'est pas courante. Néanmoins, il est nécessaire de s'en souvenir.
   • Lorsque vous enregistrez des preuves, essayez d'utiliser « nous » au lieu du pronom personnel « je ».
2. 2 Notez toutes les données d'origine. Lors de la compilation d'une preuve, la première chose à faire est de définir et d'écrire tout ce qui est donné dans le problème. Dans ce cas, vous aurez sous les yeux toutes les données initiales, sur la base desquelles il est nécessaire d'obtenir une décision. Lisez attentivement l'énoncé du problème et notez tout ce qui y est donné.
   • Par exemple : prouver que deux angles adjacents (angle A et angle B) se complètent.
   • Donné : coins adjacents A et B.
   • Démontrer que l'angle A est complémentaire de l'angle B.
3. 3 Définissez toutes les variables. En plus d'enregistrer les données d'origine, il est également utile d'écrire le reste des variables. Pour faciliter la tâche du lecteur, notez les variables au tout début de la preuve. Si aucune variable n'est définie, le lecteur peut être confus et ne pas comprendre votre preuve.
   • N'utilisez pas de variables précédemment non définies pendant la preuve.
   • Par exemple : dans le problème considéré ci-dessus, les variables sont les valeurs des angles A et B.
4. 4 Essayez de trouver la preuve dans l'ordre inverse. De nombreux problèmes sont plus faciles à résoudre dans l'ordre inverse. Commencez par ce que vous devez prouver et réfléchissez à la manière dont vous pouvez relier les conclusions à la condition initiale.
   • Relisez les étapes de début et de fin et voyez si elles se ressemblent. Pour ce faire, utilisez les conditions initiales, les définitions et les preuves similaires d'autres problèmes.
   • Posez-vous des questions et avancez. Pour prouver des déclarations individuelles, demandez-vous : « Pourquoi est-ce le cas ? » - et : "Est-ce que ça pourrait être faux ?"
   • N'oubliez pas d'écrire les étapes individuelles dans l'ordre jusqu'à ce que vous obteniez le résultat final.
   • Par exemple : si les angles A et B sont complémentaires, leur somme doit être de 180°. D'après la définition des angles adjacents, les angles A et B forment une droite ABC. Comme la ligne forme un angle de 180°, les angles A et B totalisent 180°.
5. 5 Organisez les différentes étapes de la preuve de manière à ce qu'elle soit cohérente et logique. Commencez par le début et progressez jusqu'à une thèse prouvable. Bien qu'il soit parfois utile de commencer à la fin de votre recherche de preuves, vous devez suivre le bon ordre lorsque vous les rédigez. Des thèses séparées doivent se succéder pour que la preuve soit logique et ne soulève pas de doutes.
   • Considérons d'abord les hypothèses émises.
   • Confirmez les déclarations faites avec des étapes simples et directes afin que le lecteur n'ait aucun doute sur leur exactitude.
   • Parfois, vous devez réécrire la preuve plus d'une fois. Continuez à regrouper les déclarations et leurs preuves jusqu'à ce que vous arriviez à la structure la plus logique.
   • Par exemple : commençons par le début.
     • Les angles A et B sont adjacents.
     • Les côtés du coin ABC forment une ligne droite.
     • L'angle ABC est de 180°.
     • Angle A + Angle B = Angle ABC.
     • Angle A + Angle B = Angle 180°.
     • L'angle A est complémentaire de l'angle B.
6. 6 N'utilisez pas de flèches et d'abréviations dans la preuve. Diverses abréviations et symboles peuvent être utilisés dans le projet, mais ne les incluez pas dans le projet final car cela pourrait dérouter les lecteurs. Utilisez plutôt des mots comme « donc » et « alors ».
   • À titre d'exception, les abréviations compréhensibles sont autorisées, par exemple, « ex. e." (c'est-à-dire), mais utilisez-les de manière appropriée.
7. 7 Soutenez chaque thèse avec un théorème, une loi ou une définition. La preuve doit être irréprochable. Vous ne pouvez pas faire de déclarations non fondées. Voyez comment les preuves sont construites pour des problèmes similaires aux vôtres.
   • Essayez d'appliquer les preuves que vous trouvez à des cas où cela ne devrait pas être vrai et voyez si c'est le cas. Si la preuve est valable dans de tels cas, vérifiez où vous vous êtes trompé.
   • Les preuves de problèmes géométriques sont souvent écrites en deux colonnes. Les assertions sont écrites à droite et leurs preuves sont données à gauche. Parallèlement, dans les publications, des preuves mathématiques sont rédigées sous forme de paragraphes avec la grammaire appropriée.
8. 8 Terminez les preuves par la phrase « au besoin de prouver ». A la fin de la preuve, il doit y avoir une thèse prouvable. Après cela, vous devez écrire "ce qui était nécessaire pour prouver" (abrégé en "h. Etc." ou un symbole sous la forme d'un carré plein) - cela signifie que la preuve est complète.
   • En latin, l'expression « ce qu'il fallait prouver » correspond à l'abréviation Q.E.D. (ce qu'il fallait démontrer, c'est-à-dire « ce qui devait être montré »).
   • Si vous avez des doutes sur l'exactitude de la preuve, écrivez simplement quelques phrases sur la conclusion à laquelle vous êtes parvenu et pourquoi elle est importante.

Conseils

• Toutes les informations fournies dans les preuves doivent servir à la réalisation de l'objectif déclaré. N'incluez pas ce dont vous pouvez vous passer dans votre preuve.