Contenu

• Pas
• Méthode 1 sur 3: Les bases
• Méthode 2 sur 3 : Calcul de l'incertitude de mesure multiple
• Méthode 3 sur 3: Opérations arithmétiques avec des erreurs
• Conseils
• Avertissements

Lorsque vous mesurez quelque chose, vous pouvez supposer qu'il existe une "vraie valeur" qui se situe dans la plage de valeurs que vous trouvez. Pour calculer une valeur plus précise, vous devez prendre le résultat de la mesure et l'évaluer lors de l'ajout ou de la soustraction d'une erreur. Si vous voulez savoir comment trouver une telle erreur, suivez ces étapes.

Pas

Méthode 1 sur 3: Les bases

1. 1 Exprimez correctement l'erreur. Disons que lorsque l'on mesure un bâton, sa longueur est de 4,2 cm, plus ou moins un millimètre. Cela signifie que le bâton mesure environ 4,2 cm, mais en fait, il peut être légèrement inférieur ou supérieur à cette valeur - avec une erreur pouvant aller jusqu'à un millimètre.
   • Écrivez l'erreur sous la forme : 4,2 cm ± 0,1 cm. Vous pouvez également la réécrire sous la forme 4,2 cm ± 1 mm, car 0,1 cm = 1 mm.
2. 2 Arrondissez toujours les valeurs de mesure à la même décimale que l'incertitude. Les résultats de mesure qui tiennent compte de l'incertitude sont généralement arrondis à un ou deux chiffres significatifs. Le point le plus important est que vous devez arrondir les résultats à la même décimale que l'erreur afin de maintenir la cohérence.
   • Si le résultat de la mesure est de 60 cm, l'erreur doit être arrondie au nombre entier le plus proche. Par exemple, l'erreur de cette mesure peut être de 60 cm ± 2 cm, mais pas de 60 cm ± 2,2 cm.
   • Si le résultat de la mesure est de 3,4 cm, l'erreur est arrondie à 0,1 cm. Par exemple, l'erreur de cette mesure peut être de 3,4 cm ± 0,7 cm, mais pas de 3,4 cm ± 1 cm.
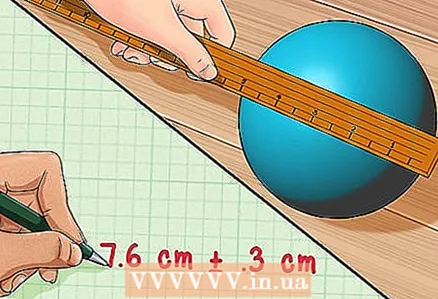3. 3 Trouvez l'erreur. Disons que vous mesurez le diamètre d'une boule ronde avec une règle. Ceci est difficile car la courbure de la balle rendra difficile la mesure de la distance entre deux points opposés sur sa surface. Disons qu'une règle peut donner un résultat avec une précision de 0,1 cm, mais cela ne signifie pas que vous pouvez mesurer le diamètre avec la même précision.
   • Examinez la boule et la règle pour avoir une idée de la précision avec laquelle vous pouvez mesurer le diamètre. La règle standard a une marque claire de 0,5 cm, mais vous pourrez peut-être mesurer le diamètre avec une plus grande précision que cela. Si vous pensez pouvoir mesurer le diamètre avec une précision de 0,3 cm, l'erreur dans ce cas est de 0,3 cm.
   • Mesurons le diamètre de la balle. Disons que vous avez une lecture d'environ 7,6 cm. Indiquez simplement le résultat de la mesure ainsi que l'erreur. Le diamètre de la boule est de 7,6 cm ± 0,3 cm.
4. 4 Calculez l'erreur en mesurant un élément parmi plusieurs. Disons que vous recevez 10 disques compacts (CD), chacun de la même taille. Disons que vous voulez trouver l'épaisseur d'un seul CD. Cette valeur est si petite que l'erreur est presque impossible à calculer.Cependant, pour calculer l'épaisseur (et son incertitude) d'un CD, vous pouvez simplement diviser la mesure (et son incertitude) de l'épaisseur des 10 CD empilés (les uns sur les autres) par le nombre total de CD.
   • Disons que la précision de la mesure d'une pile de CD à l'aide d'une règle est de 0,2 cm. Votre erreur est donc de ± 0,2 cm.
   • Disons que l'épaisseur de tous les CD est de 22 cm.
   • Divisez maintenant le résultat de la mesure et l'erreur par 10 (le nombre de tous les CD). 22 cm/10 = 2,2 cm et 0,2 cm/10 = 0,02 cm, ce qui signifie que l'épaisseur d'un CD est de 2,20 cm ± 0,02 cm.
5. 5 Mesurez plusieurs fois. Pour améliorer la précision des mesures, qu'il s'agisse de mesurer la longueur ou le temps, mesurez plusieurs fois la valeur souhaitée. Le calcul de la valeur moyenne à partir des valeurs obtenues augmentera la précision de la mesure et le calcul de l'erreur.

Méthode 2 sur 3 : Calcul de l'incertitude de mesure multiple

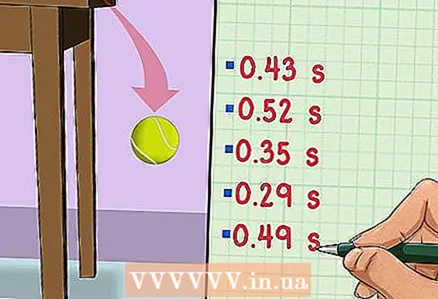1. 1 Prenez quelques mesures. Supposons que vous vouliez savoir combien de temps il faut pour que la balle tombe de la hauteur de la table. Pour de meilleurs résultats, mesurez le temps de chute un certain nombre de fois, par exemple cinq. Ensuite, vous devez trouver la moyenne des cinq mesures de temps obtenues, puis ajouter ou soustraire l'écart type pour obtenir le meilleur résultat.
   • Disons qu'à la suite de cinq mesures, les résultats sont obtenus : 0,43 s, 0,52 s, 0,35 s, 0,29 s et 0,49 s.
2. 2 Trouvez la moyenne arithmétique. Trouvez maintenant la moyenne arithmétique en additionnant cinq mesures différentes et en divisant le résultat par 5 (le nombre de mesures). 0,43 + 0,52 + 0,35 + 0,29 + 0,49 = 2,08 s. 2,08 / 5 = 0,42 s. Temps moyen 0,42 s.
3. 3 Trouver la variance des valeurs obtenues. Pour ce faire, commencez par trouver la différence entre chacune des cinq valeurs et la moyenne arithmétique. Pour ce faire, soustrayez 0,42 s de chaque résultat.
   • • 0,43 s - 0,42 s = 0,01 s
     • 0,52 s - 0,42 s = 0,1 s
     • 0,35 s - 0,42 s = -0,07 s
     • 0,29 s - 0,42 s = -0,13 s
     • 0,49 s - 0,42 s = 0,07 s
     • Ajoutez maintenant les carrés de ces différences : (0,01) + (0,1) + (-0,07) + (-0,13) + (0,07) = 0,037 s.
     • Vous pouvez trouver la moyenne arithmétique de cette somme en la divisant par 5 : 0,037 / 5 = 0,0074 s.
4. 4 Trouver l'écart type. Pour trouver l'écart type, il suffit de prendre la racine carrée de la moyenne arithmétique de la somme des carrés. La racine carrée de 0,0074 = 0,09 s, l'écart type est donc de 0,09 s.
5. 5 Écrivez votre réponse finale. Pour ce faire, enregistrez la moyenne de toutes les mesures plus ou moins l'écart type. La moyenne de toutes les mesures étant de 0,42 s et l'écart type de 0,09 s, la réponse finale est de 0,42 s ± 0,09 s.

Méthode 3 sur 3: Opérations arithmétiques avec des erreurs

1. 1 Une addition. Pour ajouter les valeurs avec des erreurs, ajoutez séparément les valeurs et séparément les erreurs.
   • (5 cm ± 0,2 cm) + (3 cm ± 0,1 cm) =
   • (5 cm + 3 cm) ± (0,2 cm + 0,1 cm) =
   • 8 cm ± 0,3 cm
2. 2 Soustraction. Pour soustraire des valeurs avec des incertitudes, soustrayez des valeurs et additionnez des incertitudes.
   • (10 cm ± 0,4 cm) - (3 cm ± 0,2 cm) =
   • (10 cm - 3 cm) ± (0,4 cm + 0,2 cm) =
   • 7 cm ± 0,6 cm
3. 3 Multiplication. Pour multiplier les valeurs avec des erreurs, multipliez les valeurs et ajoutez les erreurs RELATIVES (en pourcentage). Seule l'erreur relative peut être calculée, pas l'erreur absolue, comme c'est le cas avec l'addition et la soustraction. Pour trouver l'erreur relative, divisez l'erreur absolue par la valeur mesurée, puis multipliez par 100 pour exprimer le résultat en pourcentage. Par exemple:
   • (6 cm ± 0,2 cm) = (0,2 / 6) x 100 - l'ajout d'un signe de pourcentage donne 3,3 %.
     En conséquence:
   • (6 cm ± 0,2 cm) x (4 cm ± 0,3 cm) = (6 cm ± 3,3 %) x (4 cm ± 7,5 %)
   • (6 cm x 4 cm) ± (3,3 + 7,5) =
   • 24 cm ± 10,8 % = 24 cm ± 2,6 cm
4. 4 Division. Pour diviser les valeurs avec des incertitudes, divisez les valeurs et ajoutez les incertitudes RELATIVES.
   • (10 cm ± 0,6 cm) (5 cm ± 0,2 cm) = (10 cm ± 6 %) ÷ (5 cm ± 4 %)
   • (10 cm 5 cm) ± (6% + 4%) =
   • 2 cm ± 10 % = 2 cm ± 0,2 cm
5. 5 Exponentiation. Pour augmenter une valeur avec une erreur à une puissance, augmentez la valeur à une puissance et multipliez l'erreur relative par une puissance.
   • (2,0 cm ± 1,0 cm) =
   • (2,0 cm) ± (50 %) x 3 =
   • 8,0 cm ± 150 % ou 8,0 cm ± 12 cm

Conseils

• Vous pouvez donner une erreur à la fois pour le résultat global de toutes les mesures et pour chaque résultat d'une mesure séparément.En règle générale, les données obtenues à partir de plusieurs mesures sont moins fiables que les données obtenues directement à partir de mesures individuelles.

Avertissements

• Les sciences exactes ne fonctionnent jamais avec de "vraies" valeurs. Bien qu'une mesure correcte soit susceptible de donner une valeur dans la marge d'erreur, rien ne garantit que ce sera le cas. Les mesures scientifiques permettent l'erreur.
• Les incertitudes décrites ici ne s'appliquent qu'aux cas de distribution normale (distribution gaussienne). D'autres distributions de probabilité nécessitent des solutions différentes.