Contenu

• Pas
• Méthode 1 sur 3 : Partie 1 : Détermination du point d'inflexion
• Méthode 2 sur 3: Calcul des dérivées d'une fonction
• Méthode 3 sur 3: Partie 3: Trouver le point d'inflexion
• Conseils

En calcul différentiel, un point d'inflexion est un point sur une courbe auquel sa courbure change de signe (de plus à moins ou de moins à plus). Ce concept est utilisé en génie mécanique, en économie et en statistiques pour identifier les changements importants dans les données.

Pas

Méthode 1 sur 3 : Partie 1 : Détermination du point d'inflexion

1. 1 Définition d'une fonction concave. Le milieu de toute corde (un segment reliant deux points) du graphique d'une fonction concave se trouve soit sous le graphique, soit sur celui-ci.
2. 2 Définition d'une fonction convexe. Le milieu de toute corde (un segment reliant deux points) du graphique d'une fonction convexe se trouve soit au-dessus du graphique, soit sur celui-ci.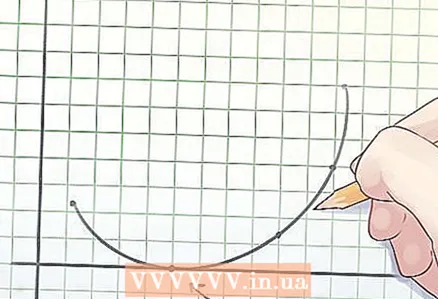
3. 3 Détermination des racines de la fonction. La racine d'une fonction est la valeur de la variable "x" à laquelle y = 0.
   • Lors du tracé d'une fonction, les racines sont les points auxquels le graphique croise l'axe des x.

Méthode 2 sur 3: Calcul des dérivées d'une fonction

1. 1 Trouvez la dérivée première de la fonction. Regardez les règles de différenciation dans le manuel ; vous devez apprendre à prendre les premières dérivées, et ensuite seulement passer à des calculs plus complexes. Les dérivées premières sont désignées par f'(x). Pour les expressions de la forme ax ^ p + bx ^ (p − 1) + cx + d, la dérivée première est : apx ^ (p − 1) + b (p - 1) x ^ (p − 2) + c.
   • Par exemple, trouvez les points d'inflexion de la fonction f (x) = x ^ 3 + 2x -1. La dérivée première de cette fonction est :
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Trouvez la dérivée seconde de la fonction. La dérivée seconde est la dérivée de la dérivée première de la fonction d'origine. La dérivée seconde est notée f ′ (x).
   • Dans l'exemple ci-dessus, la dérivée seconde est :
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 Réglez la dérivée seconde à zéro et résolvez l'équation résultante. Le résultat sera le point d'inflexion attendu.
   • Dans l'exemple ci-dessus, votre calcul ressemble à ceci :
     
     f ′ (x) = 0
     6x = 0
     x = 0
4. 4 Trouvez la dérivée troisième de la fonction. Pour vérifier que votre résultat est bien un point d'inflexion, trouvez la dérivée troisième, qui est la dérivée de la dérivée seconde de la fonction d'origine. La dérivée troisième est notée f ′ ′ (x).
   • Dans l'exemple ci-dessus, la dérivée troisième est :
     
     f ′ ′ ′ (x) = (6x) = 6

Méthode 3 sur 3: Partie 3: Trouver le point d'inflexion

1. 1 Découvrez la troisième dérivée. La règle standard pour estimer un point d'inflexion est que si la dérivée troisième n'est pas nulle (c'est-à-dire, f ′ ′ (x) 0), alors le point d'inflexion est le vrai point d'inflexion. Découvrez la dérivée troisième ; s'il n'est pas nul, alors vous avez trouvé le point d'inflexion réel.
   • Dans l'exemple ci-dessus, la dérivée troisième est 6, pas 0.Vous avez donc trouvé le vrai point d'inflexion.
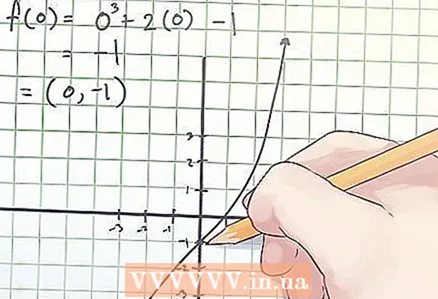2. 2 Trouvez les coordonnées du point d'inflexion. Les coordonnées du point d'inflexion sont notées (x, f (x)), où x est la valeur de la variable indépendante "x" au point d'inflexion, f (x) est la valeur de la variable dépendante "y" au point d'inflexion indiquer.
   • Dans l'exemple ci-dessus, en égalant la dérivée seconde à zéro, vous avez trouvé que x = 0. Donc, pour déterminer les coordonnées du point d'inflexion, trouvez f (0). Votre calcul ressemble à ceci :
     
     f (0) = 0 ^ 3 + 2 × 0−1 = −1.
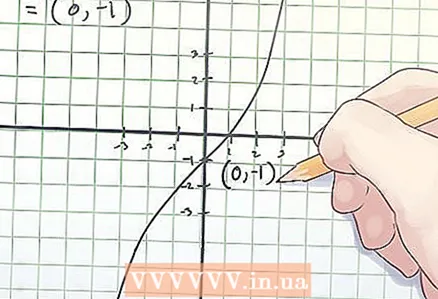3. 3 Notez les coordonnées du point d'inflexion. Les coordonnées du point d'inflexion sont les valeurs x et f (x) trouvées.
   • Dans l'exemple ci-dessus, le point d'inflexion est aux coordonnées (0, -1).

Conseils

• La dérivée première d'un terme libre (nombre premier) est toujours zéro.