Contenu

• Pas
• Méthode 1 sur 3: Comment résoudre une équation cubique sans terme constant
• Méthode 2 sur 3: Comment trouver des racines entières à l'aide de multiplicateurs
• Méthode 3 sur 3: Comment résoudre une équation à l'aide du discriminant

Dans une équation cubique, l'exposant le plus élevé est 3, une telle équation a 3 racines (solutions) et elle a la forme ${ hache displaystyle ^ {3} + bx ^ {2} + cx + d = 0}$... Certaines équations cubiques ne sont pas si faciles à résoudre, mais si vous appliquez la bonne méthode (avec une bonne base théorique), vous pouvez trouver les racines de même l'équation cubique la plus complexe - pour cela, utilisez la formule pour résoudre l'équation quadratique, trouvez le racines entières, ou calculer le discriminant.

Pas

Méthode 1 sur 3: Comment résoudre une équation cubique sans terme constant

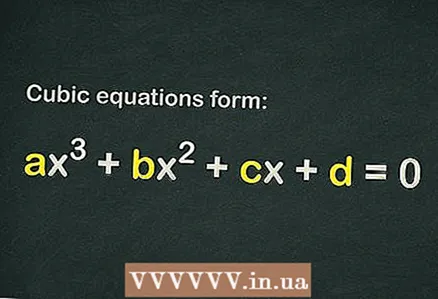1. 1 Déterminer s'il existe un terme libre dans l'équation cubique ré{ style d'affichage d}. L'équation cubique a la forme ${ hache displaystyle ^ {3} + bx ^ {2} + cx + d = 0}$... Pour qu'une équation soit considérée comme cubique, il suffit que seul le terme ${ style d'affichage x ^ {3}}$ (c'est-à-dire qu'il peut n'y avoir aucun autre membre).
   • Si l'équation a un terme libre ${ style d'affichage d}$, utilisez une autre méthode.
   • Si dans l'équation ${ style d'affichage a = 0}$, ce n'est pas cubique.
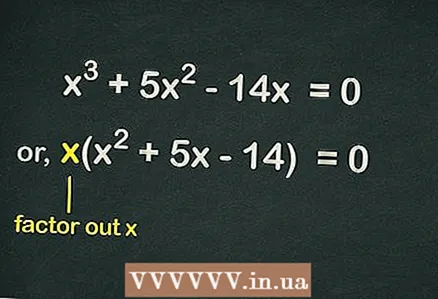2. 2 Sortez des supports X{ style d'affichage x}. Comme il n'y a pas de terme libre dans l'équation, chaque terme de l'équation inclut la variable ${ style d'affichage x}$... Cela signifie qu'un ${ style d'affichage x}$ peut être exclu des parenthèses pour simplifier l'équation. Ainsi, l'équation s'écrira ainsi : ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • Par exemple, étant donné une équation cubique ${ displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Sortir ${ style d'affichage x}$ parenthèses et obtenez ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
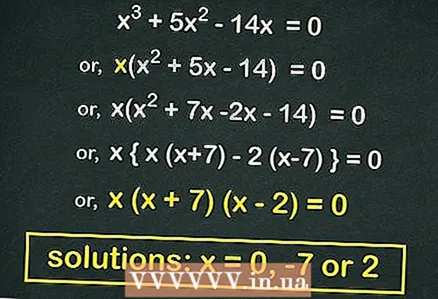3. 3 Factorisez (le produit de deux binômes) l'équation quadratique (si possible). De nombreuses équations du second degré de la forme ${ hache displaystyle ^ {2} + bx + c = 0}$ peut être factorisé. Une telle équation se révélera si nous retirons ${ style d'affichage x}$ en dehors des crochets. Dans notre exemple :
   • Sortez des supports ${ style d'affichage x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • Factoriser l'équation quadratique : ${ style d'affichage x (x + 7) (x-2) = 0}$
   • Égaliser chaque bac à ${ style d'affichage 0}$... Les racines de cette équation sont ${ style d'affichage x = 0, x = -7, x = 2}$.
4. 4 Résoudre une équation quadratique à l'aide d'une formule spéciale. Faites-le si l'équation quadratique ne peut pas être factorisée. Pour trouver deux racines d'une équation, les valeurs des coefficients ${ style d'affichage a}$, ${ style d'affichage b}$, ${ style d'affichage c}$ substitut dans la formule ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • Dans notre exemple, substituez les valeurs des coefficients ${ style d'affichage a}$, ${ style d'affichage b}$, ${ style d'affichage c}$ (${ style d'affichage 3}$, ${ style d'affichage -2}$, ${ style d'affichage 14}$) dans la formule :

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • Première racine :

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12,8i} {6}}}$

   • Deuxième racine :

     ${ displaystyle { frac {2-12,8i} {6}}}$

5. 5 Utilisez des racines nulles et quadratiques comme solutions de l'équation cubique. Les équations quadratiques ont deux racines, tandis que les équations cubiques en ont trois. Vous avez déjà trouvé deux solutions - ce sont les racines de l'équation quadratique. Si vous mettez "x" en dehors des crochets, la troisième solution serait ${ style d'affichage 0}$.
   • Si vous retirez « x » des crochets, vous obtenez ${ displaystyle x (ax ^ {2} + bx + c) = 0}$, c'est-à-dire deux facteurs : ${ style d'affichage x}$ et une équation quadratique entre parenthèses. Si l'un de ces facteurs est ${ style d'affichage 0}$, toute l'équation est également égale à ${ style d'affichage 0}$.
   • Ainsi, deux racines d'une équation quadratique sont des solutions d'une équation cubique. La troisième solution est ${ style d'affichage x = 0}$.

Méthode 2 sur 3: Comment trouver des racines entières à l'aide de multiplicateurs

1. 1 Assurez-vous qu'il y a un terme libre dans l'équation cubique ré{ style d'affichage d}. Si dans une équation de la forme ${ hache displaystyle ^ {3} + bx ^ {2} + cx + d = 0}$ il y a un membre gratuit ${ style d'affichage d}$ (qui n'est pas égal à zéro), cela ne fonctionnera pas de mettre "x" en dehors des parenthèses. Dans ce cas, utilisez la méthode décrite dans cette section.
   • Par exemple, étant donné une équation cubique ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... Pour obtenir zéro sur le côté droit de l'équation, ajoutez ${ style d'affichage 6}$ aux deux côtés de l'équation.
   • L'équation se révélera ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... Comme ${ style d'affichage d = 6}$, la méthode décrite dans la première section ne peut pas être utilisée.
2. 2 Notez les facteurs du coefficient une{ style d'affichage a} et un membre gratuit ré{ style d'affichage d}. C'est-à-dire, trouver les facteurs du nombre à ${ style d'affichage x ^ {3}}$ et les nombres avant le signe égal. Rappelez-vous que les facteurs d'un nombre sont les nombres qui, une fois multipliés, produisent ce nombre.
   • Par exemple, pour obtenir le nombre 6, il faut multiplier ${ displaystyle 6 fois 1}$ et ${ style d'affichage 2 fois 3}$... Alors les chiffres 1, 2, 3, 6 sont des facteurs du nombre 6.
   • Dans notre équation ${ style d'affichage a = 2}$ et ${ style d'affichage d = 6}$... Multiplicateurs 2 sommes 1 et 2... Multiplicateurs 6 sont les nombres 1, 2, 3 et 6.
3. 3 Divisez chaque facteur une{ style d'affichage a} pour chaque facteur ré{ style d'affichage d}. En conséquence, vous obtenez beaucoup de fractions et plusieurs nombres entiers ; les racines de l'équation cubique seront l'un des entiers ou la valeur négative de l'un des entiers.
   • Dans notre exemple, divisez les facteurs ${ style d'affichage a}$ (1 et 2) par facteurs ${ style d'affichage d}$ (1, 2, 3 et 6). Tu auras: ${ style d'affichage 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ style d'affichage 2}$ et ${ displaystyle { frac {2} {3}}}$... Ajoutez maintenant les valeurs négatives des fractions et des nombres obtenus à cette liste : ${ style d'affichage 1}$, ${ style d'affichage -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ style d'affichage 2}$, ${ style d'affichage -2}$, ${ displaystyle { frac {2} {3}}}$ et ${ displaystyle - { frac {2} {3}}}$... Les racines entières de l'équation cubique sont des nombres de cette liste.
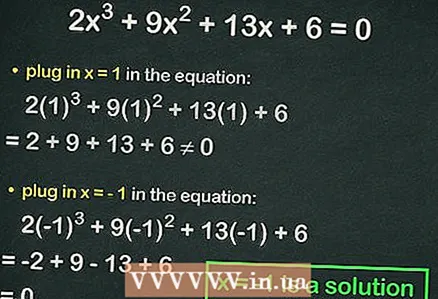4. 4 Branchez des nombres entiers dans l'équation cubique. Si l'égalité est vraie, le nombre substitué est la racine de l'équation. Par exemple, remplacez dans l'équation ${ style d'affichage 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ style d'affichage 2 + 9 + 13 + 6}$ ≠ 0, c'est-à-dire que l'égalité n'est pas respectée. Dans ce cas, branchez le numéro suivant.
   • Remplacer ${ style d'affichage -1}$: ${ style d'affichage (-2) +9 + (- 13) +6}$ = 0. Ainsi, ${ style d'affichage -1}$ est la racine entière de l'équation.
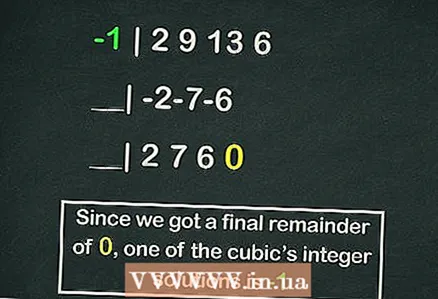5. 5 Utilisez la méthode de division des polynômes par Le schéma de Hornerpour trouver les racines de l'équation plus rapidement. Faites-le si vous ne voulez pas substituer manuellement des nombres dans l'équation. Dans le schéma de Horner, les entiers sont divisés par les valeurs des coefficients de l'équation ${ style d'affichage a}$, ${ style d'affichage b}$, ${ style d'affichage c}$ et ${ style d'affichage d}$... Si les nombres sont divisibles de manière égale (c'est-à-dire que le reste est ${ style d'affichage 0}$), un entier est la racine de l'équation.
   • Le schéma de Horner mérite un article séparé, mais ce qui suit est un exemple de calcul de l'une des racines de notre équation cubique en utilisant ce schéma :

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Donc le reste est ${ style d'affichage 0}$, mais ${ style d'affichage -1}$ est l'une des racines de l'équation.

Méthode 3 sur 3: Comment résoudre une équation à l'aide du discriminant

1. 1 Notez les valeurs des coefficients de l'équation une{ style d'affichage a}, b{ style d'affichage b}, c{ style d'affichage c} et ré{ style d'affichage d}. Nous vous recommandons de noter à l'avance les valeurs des coefficients indiqués afin de ne pas vous tromper à l'avenir.
   • Par exemple, étant donné l'équation ${ displaystyle x ^ {3} -3x ^ {2} + 3x-1}$... Écrire ${ style d'affichage a = 1}$, ${ style d'affichage b = -3}$, ${ style d'affichage c = 3}$ et ${ style d'affichage d = -1}$... Rappelez-vous que si avant ${ style d'affichage x}$ il n'y a pas de nombre, le coefficient correspondant existe toujours et est égal à ${ style d'affichage 1}$.
2. 2 Calculer le discriminant zéro en utilisant une formule spéciale. Pour résoudre une équation cubique à l'aide du discriminant, vous devez effectuer un certain nombre de calculs difficiles, mais si vous effectuez toutes les étapes correctement, cette méthode deviendra indispensable pour résoudre les équations cubiques les plus complexes. Premier calcul ${ style d'affichage Delta _ {0}}$ (zéro discriminant) est la première valeur dont nous avons besoin ; pour ce faire, substituez les valeurs correspondantes dans la formule ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • Le discriminant est un nombre qui caractérise les racines d'un polynôme (par exemple, le discriminant d'une équation quadratique est calculé par la formule ${ displaystyle b ^ {2} -4ac}$).
   • Dans notre équation :

     ${ displaystyle b ^ {2} -3ac}$

     ${ style d'affichage (-3) ^ {2} -3 (1) (3)}$

     ${ style d'affichage 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Calculer le premier discriminant à l'aide de la formule Δ1=2b3−9unebc+27une2ré{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. Premier discriminant ${ style d'affichage Delta _ {1}}$ - c'est la deuxième valeur importante ; pour le calculer, branchez les valeurs correspondantes dans la formule spécifiée.
   • Dans notre équation :

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ style d'affichage 2 (-27) -9 (-9) +27 (-1)}$

     ${ style d'affichage -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Calculer:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... Autrement dit, trouvez le discriminant de l'équation cubique à travers les valeurs obtenues ${ style d'affichage Delta _ {0}}$ et ${ style d'affichage Delta _ {1}}$... Si le discriminant d'une équation cubique est positif, l'équation a trois racines ; si le discriminant est nul, l'équation a une ou deux racines ; si le discriminant est négatif, l'équation a une racine.
   • Une équation cubique a toujours au moins une racine, puisque le graphique de cette équation coupe l'axe des X au moins en un point.
   • Dans notre équation ${ style d'affichage Delta _ {0}}$ et ${ style d'affichage Delta _ {1}}$ sont égaux ${ style d'affichage 0}$, vous pouvez donc facilement calculer ${ style d'affichage Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ style d'affichage 0-0 div 27}$

     ${ style d'affichage 0 = Delta}$... Ainsi, notre équation a une ou deux racines.

5. 5 Calculer:${ displaystyle C = ^ {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } droite) div 2}}}$. ${ style d'affichage C}$ - c'est la dernière quantité importante trouvée ; il vous aidera à calculer les racines de l'équation. Substituer les valeurs dans la formule spécifiée ${ style d'affichage Delta _ {1}}$ et ${ style d'affichage Delta _ {0}}$.
   • Dans notre équation :

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ style d'affichage 0 = C}$

6. 6 Trouvez trois racines de l'équation. Faites-le avec la formule ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, où ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, mais m est égal à 1, 2 ou alors 3... Remplacez les valeurs appropriées dans cette formule - vous obtiendrez ainsi trois racines de l'équation.
   • Calculer la valeur en utilisant la formule à m = 1, 2 ou alors 3puis vérifiez la réponse. Si vous obtenez 0 lorsque vous vérifiez votre réponse, cette valeur est la racine de l'équation.
   • Dans notre exemple, remplacez 1 dans ${ displaystyle x ^ {3} -3x ^ {2} + 3x-1}$ et obtenir 0, c'est à dire 1 est l'une des racines de l'équation.