Contenu

• Pas

Une équation trigonométrique contient une ou plusieurs fonctions trigonométriques de la variable "x" (ou de toute autre variable). Résoudre une équation trigonométrique, c'est trouver une telle valeur "x" qui satisfasse la ou les fonctions et l'équation dans son ensemble.

• Les solutions des équations trigonométriques sont exprimées en degrés ou en radians. Exemples:

x = / 3; x = 5π / 6 ; x = 3π/2 ; x = 45 degrés ; x = 37,12 degrés ; x = 178,37 degrés.

• Remarque : les valeurs des fonctions trigonométriques des angles, exprimés en radians, et des angles, exprimés en degrés, sont égales. Un cercle trigonométrique de rayon égal à un est utilisé pour décrire les fonctions trigonométriques, ainsi que pour vérifier l'exactitude de la solution des équations et inégalités trigonométriques de base.
• Exemples d'équations trigonométriques :
  • sin x + sin 2x = 1/2; tg x + ctg x = 1,732 ;
  • cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.

1. Un cercle trigonométrique de rayon un (cercle unitaire).
   • C'est un cercle de rayon égal à un et de centre au point O. Le cercle unitaire décrit 4 fonctions trigonométriques de base de la variable "x", où "x" est l'angle mesuré à partir de la direction positive de l'axe X dans le sens inverse des aiguilles d'une montre.
   • Si « x » est un angle sur le cercle unité, alors :
   • L'axe horizontal OAx définit la fonction F (x) = cos x.
   • L'axe vertical OBy définit la fonction F (x) = sin x.
   • L'axe vertical AT définit la fonction F (x) = tan x.
   • L'axe horizontal BU définit la fonction F(x) = ctg x.

• Le cercle unitaire est également utilisé pour résoudre des équations et des inégalités trigonométriques de base (différentes positions de "x" y sont prises en compte).

Pas

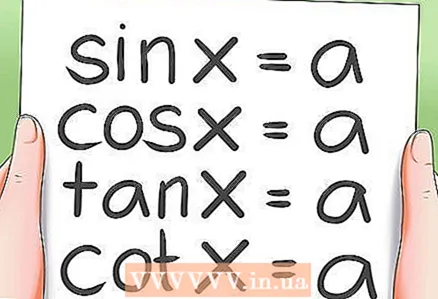1. 1 Le concept de résolution d'équations trigonométriques.
   • Pour résoudre une équation trigonométrique, convertissez-la en une ou plusieurs équations trigonométriques de base. Résoudre une équation trigonométrique revient finalement à résoudre quatre équations trigonométriques de base.
2. 2 Résolution d'équations trigonométriques de base.
   • Il existe 4 types d'équations trigonométriques de base :
   • sin x = a; cos x = un
   • tg x = a; ctg x = un
   • Résoudre des équations trigonométriques de base consiste à examiner les différentes positions x sur le cercle unité et à utiliser une table de conversion (ou une calculatrice).
   • Exemple 1.sin x = 0,866. En utilisant une table de conversion (ou une calculatrice), vous obtenez la réponse : x = π / 3. Le cercle unité donne une autre réponse : 2π / 3. N'oubliez pas que toutes les fonctions trigonométriques sont périodiques, c'est-à-dire que leurs valeurs sont répétées. Par exemple, la périodicité de sin x et cos x est 2πn, et la périodicité de tg x et ctg x est πn. La réponse s'écrit donc ainsi :
   • x1 = / 3 + 2πn; x2 = 2π / 3 + 2πn.
   • Exemple 2.cos x = -1/2. En utilisant une table de conversion (ou une calculatrice), vous obtenez la réponse : x = 2π / 3. Le cercle unité donne une autre réponse : -2π / 3.
   • x1 = 2π / 3 + 2π ; x2 = -2π / 3 + 2π.
   • Exemple 3.tg (x - π / 4) = 0.
   • Réponse : x = / 4 + πn.
   • Exemple 4. ctg 2x = 1,732.
   • Réponse : x = / 12 + n.
3. 3 Transformations utilisées pour résoudre des équations trigonométriques.
   • Pour transformer des équations trigonométriques, des transformations algébriques (factorisation, réduction de termes homogènes, etc.) et des identités trigonométriques sont utilisées.
   • Exemple 5. En utilisant des identités trigonométriques, l'équation sin x + sin 2x + sin 3x = 0 est transformée en l'équation 4cos x * sin (3x / 2) * cos (x / 2) = 0. Ainsi, vous devez résoudre les équations trigonométriques de base suivantes : cos x = 0 ; péché (3x / 2) = 0; cos (x / 2) = 0.
     
     
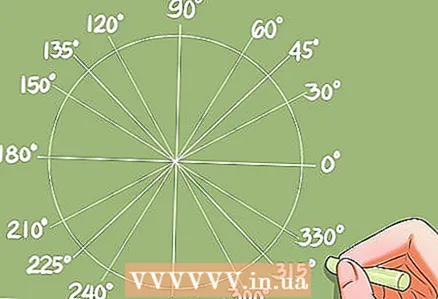4. 4 Trouver des angles à partir de valeurs connues de fonctions.
   • Avant d'apprendre des méthodes de résolution d'équations trigonométriques, vous devez apprendre à trouver des angles à partir de valeurs connues de fonctions. Cela peut être fait à l'aide d'une table de conversion ou d'une calculatrice.
   • Exemple : cosx = 0,732. La calculatrice donnera la réponse x = 42,95 degrés. Le cercle unité donnera des angles supplémentaires, dont le cosinus est également de 0,732.
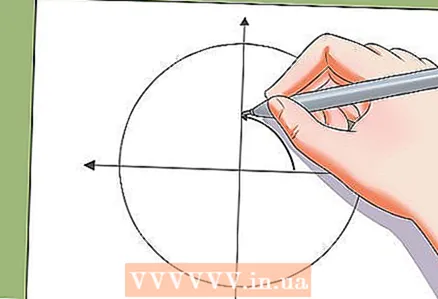5. 5 Mettez la solution de côté sur le cercle de l'unité.
   • Vous pouvez reporter les solutions de l'équation trigonométrique sur le cercle unité. Les solutions de l'équation trigonométrique sur le cercle unité sont les sommets d'un polygone régulier.
   • Exemple : Les solutions x = π / 3 + πn / 2 sur le cercle unité sont les sommets d'un carré.
   • Exemple : Les solutions x = π / 4 + πn / 3 sur le cercle unité représentent les sommets d'un hexagone régulier.
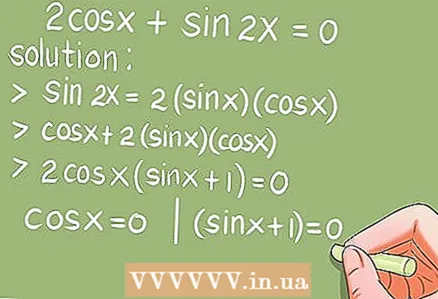6. 6 Méthodes de résolution des équations trigonométriques.
   • Si une équation trigonométrique donnée ne contient qu'une seule fonction trigonométrique, résolvez cette équation en tant qu'équation trigonométrique de base.Si une équation donnée comprend deux ou plusieurs fonctions trigonométriques, il existe alors 2 méthodes pour résoudre une telle équation (selon la possibilité de sa transformation).
     • Méthode 1.
   • Convertissez cette équation en une équation de la forme : f (x) * g (x) * h (x) = 0, où f (x), g (x), h (x) sont les équations trigonométriques de base.
     
     
   • Exemple 6.2cos x + sin 2x = 0. (0 x 2π)
   • Solution. En utilisant la formule du double angle sin 2x = 2 * sin x * cos x, remplacez sin 2x.
   • 2cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Résolvez maintenant les deux équations trigonométriques de base : cos x = 0 et (sin x + 1) = 0.
   • Exemple 7.cos x + cos 2x + cos 3x = 0. (0 x 2π)
   • Solution : À l'aide d'identités trigonométriques, transformez cette équation en une équation de la forme : cos 2x (2cos x + 1) = 0. Résolvez maintenant les deux équations trigonométriques de base : cos 2x = 0 et (2cos x + 1) = 0.
   • Exemple 8.sin x - sin 3x = cos 2x. (0 x 2π)
   • Solution : À l'aide d'identités trigonométriques, transformez cette équation en une équation de la forme : -cos 2x * (2sin x + 1) = 0. Résolvez maintenant les deux équations trigonométriques de base : cos 2x = 0 et (2sin x + 1) = 0.
     • Méthode 2.
   • Convertir l'équation trigonométrique donnée en une équation contenant une seule fonction trigonométrique. Remplacez ensuite cette fonction trigonométrique par une inconnue, par exemple, t (sin x = t; cos x = t; cos 2x = t, tg x = t; tg (x / 2) = t, etc.).
   • Exemple 9.3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2π).
   • Solution. Dans cette équation, remplacez (cos ^ 2 x) par (1 - sin ^ 2 x) (par identité). L'équation transformée est :
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Remplacez sin x par t. L'équation ressemble maintenant à ceci : 5t ^ 2 - 4t - 9 = 0. C'est une équation quadratique avec deux racines : t1 = -1 et t2 = 9/5. La seconde racine t2 ne satisfait pas la plage de valeurs de la fonction (-1 sin x 1). Décidez maintenant : t = sin x = -1 ; x = 3π / 2.
   • Exemple 10.tg x + 2 tg ^ 2 x = ctg x + 2
   • Solution. Remplacez tg x par t. Réécrivez l'équation originale comme suit : (2t + 1) (t ^ 2 - 1) = 0. Trouvez maintenant t puis trouvez x pour t = tg x.
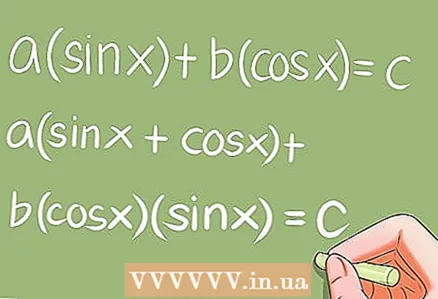7. 7 Équations trigonométriques spéciales.
   • Il existe plusieurs équations trigonométriques spéciales qui nécessitent des transformations spécifiques. Exemples:
   • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
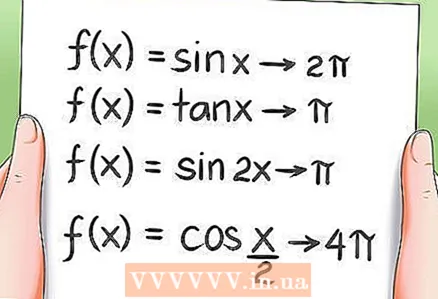8. 8 Périodicité des fonctions trigonométriques.
   • Comme mentionné précédemment, toutes les fonctions trigonométriques sont périodiques, c'est-à-dire que leurs valeurs sont répétées après une certaine période. Exemples:
     • La période de la fonction f (x) = sin x est 2π.
     • La période de la fonction f (x) = tan x est égale à .
     • La période de la fonction f (x) = sin 2x est .
     • La période de la fonction f (x) = cos (x / 2) est de 4π.
   • Si la période est spécifiée dans le problème, calculez la valeur « x » dans cette période.
   • Remarque : La résolution d'équations trigonométriques n'est pas une tâche facile et conduit souvent à des erreurs. Vérifiez donc bien vos réponses. Pour ce faire, vous pouvez utiliser une calculatrice graphique pour tracer l'équation donnée R (x) = 0. Dans de tels cas, les solutions seront présentées sous forme de fractions décimales (c'est-à-dire que π est remplacé par 3,14).