Contenu

• Avancer d'un pas
• Partie 1 sur 4: Élaboration de la matrice
• Partie 2 sur 4: Apprentissage des opérations de résolution d'un système avec une matrice
• Partie 3 sur 4: Fusionnez les étapes pour résoudre la galaxie
• Partie 4 sur 4: Vérification de votre solution
• Conseils

Une matrice est un moyen très utile de représenter des nombres dans un format de bloc, que vous pouvez ensuite utiliser pour résoudre un système d'équations linéaires. Si vous n'avez que deux variables, vous utiliserez probablement une méthode différente. Lisez à ce sujet dans Résolution d'un système d'équations pour des exemples de ces autres méthodes. Mais si vous avez trois variables ou plus, un tableau est idéal. En utilisant des combinaisons répétées de multiplication et d'addition, vous pouvez systématiquement arriver à une solution.

Avancer d'un pas

Partie 1 sur 4: Élaboration de la matrice

1. Vérifiez que vous disposez de suffisamment de données. Pour obtenir une solution unique pour chaque variable d'un système linéaire à l'aide d'une matrice, vous devez avoir autant d'équations que le nombre de variables que vous essayez de résoudre. Par exemple: avec les variables x, y et z, vous avez besoin de trois équations. Si vous avez quatre variables, vous avez besoin de quatre équations.
   • Si vous avez moins d'équations que le nombre de variables, vous découvrirez certaines limites des variables (telles que x = 3y et y = 2z), mais vous ne pouvez pas obtenir une solution précise. Pour cet article, nous travaillerons uniquement vers une solution unique.
2. Écrivez vos équations sous la forme standard. Avant de pouvoir mettre les données des équations sous forme matricielle, vous devez d'abord écrire chaque équation sous forme standard. La forme standard d'une équation linéaire est Ax + By + Cz = D, où les lettres majuscules sont les coefficients (nombres) et le dernier nombre (D dans cet exemple) est à droite du signe égal.
   • Si vous avez plus de variables, continuez simplement la ligne aussi longtemps que nécessaire. Par exemple, si vous essayiez de résoudre un système avec six variables, votre forme par défaut ressemblerait à Au + Bv + Cw + Dx + Ey + Fz = G. Dans cet article, nous nous concentrerons sur les systèmes avec seulement trois variables. Résoudre une galaxie plus grande est exactement la même chose, mais prend juste plus de temps et plus d'étapes.
   • Notez que sous forme standard, les opérations entre les termes sont toujours un ajout. S'il y a une soustraction dans votre équation, au lieu d'une addition, vous devrez travailler avec cela plus tard en rendant votre coefficient négatif. Pour rendre cela plus facile à retenir, vous pouvez réécrire l'équation et ajouter l'opération et rendre le coefficient négatif. Par exemple, vous pouvez réécrire l'équation 3x-2y + 4z = 1 comme 3x + (- 2y) + 4z = 1.
3. Placez les nombres du système d'équations dans une matrice. Une matrice est un groupe de nombres, disposés dans une sorte de tableau, avec lequel nous allons travailler pour résoudre le système. Il contient essentiellement les mêmes données que les équations elles-mêmes, mais dans un format plus simple. Pour créer la matrice de vos équations sous forme standard, copiez simplement les coefficients et le résultat de chaque équation dans une seule ligne et empilez ces lignes les unes sur les autres.
   • Supposons que vous ayez un système composé des trois équations 3x + y-z = 9, 2x-2y + z = -3 et x + y + z = 7. La rangée supérieure de votre matrice contiendra les nombres 3, 1, -1, 9, car ce sont les coefficients et la solution de la première équation. Notez que toute variable qui n'a pas de coefficient est supposée avoir un coefficient de 1. La deuxième ligne de la matrice devient 2, -2, 1, -3 et la troisième ligne devient 1, 1, 1, 7.
   • Assurez-vous d'aligner les coefficients x dans la première colonne, les coefficients y dans la seconde, les coefficients z dans la troisième et les termes de solution dans la quatrième. Lorsque vous avez terminé de travailler avec la matrice, ces colonnes seront importantes lors de l'écriture de votre solution.
4. Dessinez une grande parenthèse carrée autour de votre matrice entière. Par convention, une matrice est indiquée par une paire de crochets, [], autour du bloc entier de nombres. Les crochets n'affectent en aucun cas la solution, mais ils indiquent que vous travaillez avec des matrices. Une matrice peut être constituée de n'importe quel nombre de lignes et de colonnes. Dans cet article, nous utiliserons des parenthèses autour des termes dans une ligne pour indiquer qu'ils appartiennent ensemble.
5. Utilisation du symbolisme commun. Lorsque vous travaillez avec des matrices, il est courant de faire référence aux lignes avec l'abréviation R et aux colonnes avec l'abréviation C. Vous pouvez utiliser des nombres avec ces lettres pour indiquer une ligne ou une colonne spécifique. Par exemple, pour indiquer la ligne 1 d'une matrice, vous pouvez écrire R1. La ligne 2 devient alors R2.
   • Vous pouvez indiquer n'importe quelle position spécifique dans une matrice en utilisant une combinaison de R et C. Par exemple, pour indiquer un terme dans la deuxième ligne, la troisième colonne, vous pouvez l'appeler R2C3.

Partie 2 sur 4: Apprentissage des opérations de résolution d'un système avec une matrice

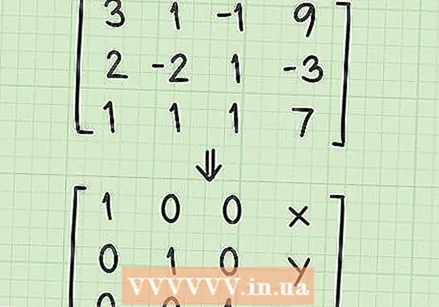1. Comprenez la forme de la matrice de solution. Avant de commencer à résoudre votre système d'équations, vous devez comprendre ce que vous allez faire avec la matrice. À ce stade, vous avez une matrice qui ressemble à ceci:
   • 3 1 -1 9
   • 2 -2 1 -3
   • 1 1 1 7
   • Vous travaillez avec un certain nombre d'opérations de base pour créer la «matrice de solution». La matrice de solution ressemblera à ceci:
   • 1 0 0 x
   • 0 1 0 ans
   • 0 0 1 z
   • Notez que la matrice se compose de 1 sur une ligne diagonale avec des 0 dans tous les autres espaces sauf la quatrième colonne. Les nombres de la quatrième colonne sont la solution pour les variables x, y et z.
2. Utilisez la multiplication scalaire. Le premier outil à votre disposition pour résoudre un système à l'aide d'une matrice est la multiplication scalaire. C'est simplement un terme qui signifie que vous multipliez les éléments d'une ligne de la matrice par un nombre constant (pas une variable). Lorsque vous utilisez la multiplication scalaire, gardez à l'esprit que vous devez multiplier chaque terme de la ligne entière par le nombre que vous sélectionnez. Si vous oubliez le premier terme et que vous multipliez simplement, vous obtiendrez la mauvaise solution. Cependant, vous n'êtes pas obligé de multiplier la matrice entière en même temps. Dans la multiplication scalaire, vous ne travaillez que sur une ligne à la fois.
   • Il est courant d'utiliser des fractions dans la multiplication scalaire, car vous souhaitez souvent obtenir une ligne diagonale de 1. Habituez-vous à travailler avec des fractions. Il sera également plus facile (pour la plupart des étapes de résolution de la matrice) de pouvoir écrire vos fractions sous une forme incorrecte, puis de les reconvertir en nombres mixtes pour la solution finale. Par conséquent, le nombre 1 2/3 est plus facile à utiliser si vous l'écrivez comme 5/3.
   • Par exemple, la première ligne (R1) de notre exemple de problème commence par les termes [3,1, -1,9]. La matrice de solution doit contenir un 1 dans la première position de la première ligne. Pour "changer" le 3 en 1, nous pouvons multiplier la ligne entière par 1/3. Cela crée le nouveau R1 de [1,1 / 3, -1 / 3,3].
   • Assurez-vous de laisser tous les signes négatifs à leur place.
3. Utilisez l'addition de lignes ou la soustraction de lignes. Le deuxième outil que vous pouvez utiliser est d'ajouter ou de soustraire deux lignes de la matrice. Pour créer les termes 0 dans votre matrice de solution, vous devez ajouter ou soustraire des nombres pour atteindre le 0. Par exemple, si R1 est d'une matrice [1,4,3,2] et R2 est [1,3,5,8], vous pouvez soustraire la première ligne de la deuxième ligne et créer une nouvelle ligne [0, -1, 2,6], car 1-1 = 0 (première colonne), 3-4 = -1 (deuxième colonne), 5-3 = 2 (troisième colonne) et 8-2 = 6 (quatrième colonne). Lorsque vous effectuez une addition ou une soustraction de lignes, réécrivez votre nouveau résultat au lieu de la ligne avec laquelle vous avez commencé. Dans ce cas, nous extraire la ligne 2 et insérer la nouvelle ligne [0, -1,2,6].
   • Vous pouvez utiliser une notation abrégée et déclarer cette action comme R2-R1 = [0, -1,2,6].
   • N'oubliez pas que l'addition et la soustraction sont des formes opposées de la même opération. Pensez-y comme ajouter deux nombres ou soustraire le contraire. Par exemple, si vous commencez par l'équation simple 3-3 = 0, vous pouvez considérer cela comme un problème d'addition de 3 + (- 3) = 0. Le résultat est le même. Cela semble simple, mais il est parfois plus facile d'envisager un problème sous une forme ou une autre. Gardez simplement un œil sur vos signes négatifs.
4. Combinez l'addition de lignes et la multiplication scalaire en une seule étape. Vous ne pouvez pas vous attendre à ce que les termes correspondent toujours, vous pouvez donc utiliser une simple addition ou soustraction pour créer des 0 dans votre matrice. Le plus souvent, vous devrez ajouter (ou soustraire) un multiple d'une autre ligne. Pour ce faire, effectuez d'abord la multiplication scalaire, puis ajoutez ce résultat à la ligne cible que vous essayez de modifier.
   • Supposer; qu'il existe une ligne 1 de [1,1,2,6] et une ligne 2 de [2,3,1,1]. Vous voulez un terme 0 dans la première colonne de R2. Autrement dit, vous voulez changer le 2 en un 0. Pour ce faire, vous devez soustraire un 2. Vous pouvez obtenir un 2 en multipliant d'abord la ligne 1 par la multiplication scalaire 2, puis en soustrayant la première ligne de la deuxième ligne. En bref, cela peut être écrit comme R2-2 * R1. Tout d'abord, multipliez R1 par 2 pour obtenir [2,2,4,12]. Puis soustrayez ceci de R2 pour obtenir [(2-2), (3-2), (1-4), (1-12)]. Simplifiez cela et votre nouveau R2 sera [0,1, -3, -11].
5. Copiez les lignes qui restent inchangées pendant que vous travaillez. Au fur et à mesure que vous travaillez sur la matrice, vous modifiez une seule ligne à la fois, soit par multiplication scalaire, addition de lignes ou soustraction de lignes, soit par une combinaison d'étapes. Lorsque vous modifiez une ligne, assurez-vous de copier les autres lignes de votre matrice dans leur forme d'origine.
   • Une erreur courante se produit lors de l'exécution d'une étape combinée de multiplication et d'addition en un seul mouvement. Par exemple, disons que vous devez soustraire R1 de R2 deux fois. Lorsque vous multipliez R1 par 2 pour faire cette étape, rappelez-vous que R1 ne change pas dans la matrice. Vous ne faites la multiplication que pour changer R2. Copiez d'abord R1 dans sa forme d'origine, puis modifiez R2.
6. Premier travail de haut en bas. Pour résoudre le système, vous travaillez selon un modèle très organisé, essentiellement en «résolvant» un terme de la matrice à la fois. La séquence d'un tableau à trois variables ressemblera à ceci:
   • 1. Faites un 1 dans la première ligne, première colonne (R1C1).
   • 2. Faites un 0 dans la deuxième ligne, première colonne (R2C1).
   • 3. Faites un 1 dans la deuxième ligne, deuxième colonne (R2C2).
   • 4. Faites un 0 dans la troisième ligne, première colonne (R3C1).
   • 5. Faites un 0 dans la troisième ligne, deuxième colonne (R3C2).
   • 6. Faites un 1 dans la troisième ligne, troisième colonne (R3C3).
7. Revenez de bas en haut. À ce stade, si vous avez effectué les étapes correctement, vous êtes à mi-chemin de la solution. Vous devez avoir la ligne diagonale de 1, avec des 0 en dessous. Les nombres de la quatrième colonne n'ont pas d'importance à ce stade. Maintenant, vous revenez au sommet comme suit:
   • Créez un 0 dans la deuxième ligne, troisième colonne (R2C3).
   • Créez un 0 dans la première ligne, troisième colonne (R1C3).
   • Créez un 0 dans la première ligne, deuxième colonne (R1C2).
8. Vérifiez si vous avez créé la matrice de solution. Si votre travail est correct, vous avez créé la matrice de solution avec des 1 dans une ligne diagonale de R1C1, R2C2, R3C3 et des 0 dans les autres positions des trois premières colonnes. Les nombres de la quatrième colonne sont les solutions pour votre système linéaire.

Partie 3 sur 4: Fusionnez les étapes pour résoudre la galaxie

1. Commencez par un exemple de système d'équations linéaires. Pour pratiquer ces étapes, commençons par le système que nous avons utilisé précédemment: 3x + y-z = 9, 2x-2y + z = -3 et x + y + z = 7. Si vous écrivez ceci dans une matrice, vous avez R1 = [3,1, -1,9], R2 = [2, -2,1, -3] et R3 = [1,1,1,7].
2. Créez un 1 dans la première position R1C1. Notez que R1 commence par un 3 à ce stade, vous devez le changer en 1. Vous pouvez le faire par multiplication scalaire, en multipliant les quatre termes de R1 par 1/3. En abrégé, vous pouvez écrire comme R1 * 1/3. Cela donne un nouveau résultat pour R1 si R1 = [1,1 / 3, -1 / 3,3]. Copiez R2 et R2, inchangés, lorsque R2 = [2, -2,1, -3] et R3 = [1,1,1,7].
   • Notez que la multiplication et la division ne sont que des fonctions inverses l'une de l'autre. On peut dire que l'on multiplie par 1/3 ou on divise par 3, sans changer le résultat.
3. Créez un 0 dans la deuxième ligne, première colonne (R2C1). À ce stade, R2 = [2, -2,1, -3]. Pour vous rapprocher de la matrice de solution, vous devez changer le premier terme de 2 en 0. Vous pouvez le faire en soustrayant deux fois la valeur de R1, puisque R1 commence par un 1. En abrégé, l'opération R2- 2 * R1. N'oubliez pas que vous ne changez pas R1, travaillez simplement avec. Copiez donc d'abord R1 si R1 = [1,1 / 3, -1 / 3,3]. Ensuite, si vous doublez chaque terme de R1, vous obtenez 2 * R1 = [2,2 / 3, -2 / 3,6]. Enfin, soustrayez ce résultat du R2 d'origine pour obtenir votre nouveau R2. Terme de travail par terme, cette soustraction devient (2-2), (-2-2 / 3), (1 - (- 2/3)), (-3-6). Nous simplifions ces derniers au nouveau R2 = [0, -8 / 3,5 / 3, -9]. Notez que le premier terme est 0 (quel que soit votre objectif).
   • Écrivez la ligne 3 (qui n'a pas changé) comme R3 = [1,1,1,7].
   • Soyez prudent lorsque vous soustrayez des nombres négatifs pour vous assurer que les signes restent corrects.
   • Maintenant, laissons d'abord les fractions sous leur forme incorrecte. Cela facilite les étapes ultérieures de la solution. Vous pouvez simplifier les fractions dans la dernière étape du problème.
4. Créez un 1 dans la deuxième ligne, deuxième colonne (R2C2). Pour continuer à former la ligne diagonale des 1, vous devez convertir le deuxième terme -8/3 en 1. Pour ce faire, multipliez la ligne entière par l'inverse de ce nombre (-3/8). Symboliquement, cette étape est R2 * (- 3/8). La deuxième ligne résultante est R2 = [0,1, -5 / 8,27 / 8].
   • Notez que si la moitié gauche de la ligne commence à ressembler à la solution avec le 0 et le 1, la moitié droite peut commencer à avoir l'air moche, avec des fractions incorrectes. Laissez-les pour ce qu'ils sont pour le moment.
   • N'oubliez pas de continuer à copier les lignes intactes, donc R1 = [1,1 / 3, -1 / 3,3] et R3 = [1,1,1,7].
5. Créez un 0 dans la troisième ligne, première colonne (R3C1). Votre focus se déplace maintenant sur la troisième ligne, R3 = [1,1,1,7]. Pour faire un 0 dans la première position, vous devez soustraire un 1 du 1 actuellement dans cette position. Si vous regardez vers le haut, il y a un 1 sur la première position de R1. Il vous suffit donc de soustraire R1 de R3 pour obtenir le résultat dont vous avez besoin. Durée de travail pour terme, cela devient (1-1), (1-1 / 3), (1 - (- 1/3)), (7-3). Ces quatre mini-problèmes peuvent alors être simplifiés au nouveau R3 = [0,2 / 3,4 / 3,4].
   • Continuez à copier le long de R1 = [1,1 / 3, -1 / 3,3] et R2 = [0,1, -5 / 8,27 / 8]. N'oubliez pas que vous ne modifiez qu'une seule ligne à la fois.
6. Faites un 0 dans la troisième ligne, deuxième colonne (R3C2). Cette valeur est actuellement de 2/3, mais doit être convertie en 0. À première vue, il semble que vous puissiez soustraire les valeurs de R1 par double, car la colonne correspondante de R1 contient un 1/3. Cependant, si vous doublez et soustrayez toutes les valeurs de R1, le 0 dans la première colonne de R3 change, ce que vous ne voulez pas. Ce serait un pas en arrière dans votre solution. Vous devez donc travailler avec une combinaison de R2. Soustraire 2/3 de R2 crée un 0 dans la deuxième colonne, sans changer la première colonne. En bref, il s'agit de R3-2 / 3 * R2. Les termes individuels deviennent (0-0), (2 / 3-2 / 3), (4/3 - (- 5/3 * 2/3)), (4-27 / 8 * 2/3) . La simplification donne alors R3 = [0,0,42 / 24,42 / 24].
7. Créez un 1 dans la troisième ligne, troisième colonne (R3C3). Il s'agit d'une simple multiplication par l'inverse du nombre indiqué. La valeur actuelle est 42/24, vous pouvez donc multiplier par 24/42 pour obtenir la valeur souhaitée 1. Notez que les deux premiers termes sont tous les deux 0, donc toute multiplication reste 0. La nouvelle valeur de R3 = [0,0,1,1].
   • Notez que les fractions qui semblaient assez compliquées à l'étape précédente commencent déjà à se résoudre.
   • Continuez avec R1 = [1,1 / 3, -1 / 3,3] et R2 = [0,1, -5 / 8,27 / 8].
   • Notez qu'à ce stade, vous avez la diagonale de 1 pour votre matrice de solution. Il vous suffit de convertir trois éléments de la matrice en 0 pour trouver votre solution.
8. Créez un 0 dans la deuxième ligne, troisième colonne. R2 est actuellement [0,1, -5 / 8,27 / 8], avec une valeur de -5/8 dans la troisième colonne. Vous devez le transformer en 0. Cela signifie que vous devez effectuer une opération avec R3 qui consiste à ajouter 5/8. Puisque la troisième colonne correspondante de R3 est un 1, vous devez multiplier toutes les valeurs de R3 par 5/8 et ajouter le résultat à R2. En bref, c'est R2 + 5/8 * R3. Terme pour terme c'est R2 = (0 + 0), (1 + 0), (-5 / 8 + 5/8), (27/8 + 5/8). Cela peut être simplifié en R2 = [0,1,0,4].
   • Copiez ensuite R1 = [1,1 / 3, -1 / 3,3] et R3 = [0,0,1,1].
9. Créez un 0 dans la première ligne, troisième colonne (R1C3). La première ligne est actuellement R1 = [1,1 / 3, -1 / 3,3]. Vous devez convertir le -1/3 de la troisième colonne en un 0, en utilisant une combinaison de R3. Vous ne voulez pas utiliser R2, car le 1 dans la deuxième colonne de R2 changerait R1 dans le mauvais sens. Vous multipliez donc R3 * 1/3 et ajoutez le résultat à R1. La notation pour cela est R1 + 1/3 * R3. Le terme d'élaboration des termes donne R1 = (1 + 0), (1/3 + 0), (-1 / 3 + 1/3), (3 + 1/3). Vous pouvez simplifier cela avec un nouveau R1 = [1,1 / 3,0,10 / 3].
   • Copiez les R2 = [0,1,0,4] et R3 = [0,0,1,1] inchangés.
10. Faites un 0 dans la première ligne, deuxième colonne (R1C2). Si tout est fait correctement, cela devrait être la dernière étape. Vous devez convertir 1/3 de la deuxième colonne en un 0. Vous pouvez l'obtenir en multipliant et en soustrayant R2 * 1/3. En bref, il s'agit de R1-1 / 3 * R2. Le résultat est R1 = (1-0), (1 / 3-1 / 3), (0-0), (10 / 3-4 / 3). La simplification donne alors R1 = [1,0,0,2].
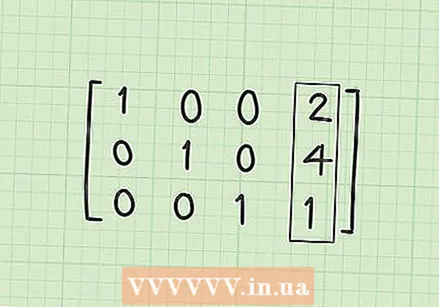11. Recherchez la matrice de solution. À ce stade, si tout s'est bien passé, vous auriez les trois lignes R1 = [1,0,0,2], R2 = [0,1,0,4] et R3 = [0,0,1,1] dois avoir. Notez que si vous écrivez ceci sous forme de matrice de blocs avec les lignes les unes au-dessus des autres, vous avez des 1 diagonaux avec des 0 plus loin, et vos solutions sont dans la quatrième colonne. La matrice de solution devrait ressembler à ceci:
    • 1 0 0 2
    • 0 1 0 4
    • 0 0 1 1
12. Comprendre votre solution. Après avoir converti les équations linéaires en matrice, vous mettez les coefficients x dans la première colonne, les coefficients y dans la deuxième colonne, les coefficients z dans la troisième colonne. Si vous souhaitez réécrire à nouveau la matrice en équations, ces trois lignes de la matrice signifient en fait les trois équations 1x + 0y + 0z = 2, 0x + 1y + 0z = 4 et 0x + 0y + 1z = 1. Puisque nous pouvons rayer les termes 0 et ne pas avoir à écrire les 1 coefficients, ces trois équations se simplifient à la solution, x = 2, y = 4 et z = 1. C'est la solution à votre système d'équations linéaires.

Partie 4 sur 4: Vérification de votre solution

1. Incluez les solutions dans chaque variable de chaque équation. C'est toujours une bonne idée de vérifier que votre solution est réellement correcte. Pour ce faire, testez vos résultats dans les équations d'origine.
   • Les équations originales de ce problème étaient: 3x + y-z = 9, 2x-2y + z = -3 et x + y + z = 7. Lorsque vous remplacez les variables par leurs valeurs que vous avez trouvées, vous obtenez 3 * 2 + 4-1 = 9, 2 * 2-2 * 4 + 1 = -3 et 2 + 4 + 1 = 7.
2. Simplifiez toute comparaison. Effectuez les opérations dans chaque équation selon les règles de base des opérations. La première équation se simplifie à 6 + 4-1 = 9, ou 9 = 9. La deuxième équation peut être simplifiée en 4-8 + 1 = -3 ou -3 = -3. La dernière équation est simplement 7 = 7.
   • Étant donné que toute équation se simplifie en un vrai énoncé mathématique, vos solutions sont correctes. Si l'une des solutions est incorrecte, vérifiez à nouveau votre travail et recherchez d'éventuelles erreurs. Certaines erreurs courantes se produisent lorsque vous vous débarrassez des signes moins en cours de route ou que vous confondez la multiplication et l'addition de fractions.
3. Écrivez vos solutions finales. Pour ce problème donné, la solution finale est x = 2, y = 4 et z = 1.

Conseils

• Si votre système d'équations est très complexe, avec de nombreuses variables, vous pourrez peut-être utiliser une calculatrice graphique au lieu de faire le travail à la main. Pour plus d'informations à ce sujet, vous pouvez également consulter wikiHow.