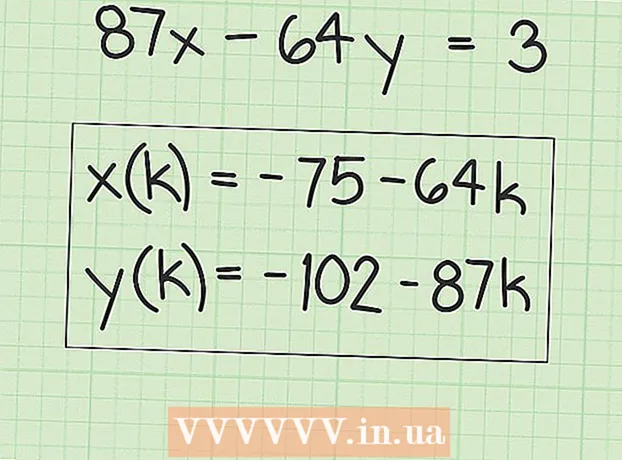
Contenu

• Pas
• Partie 1 sur 4: Comment écrire une équation
• Partie 2 sur 4: Comment écrire l'algorithme d'Euclide
• Partie 3 sur 4: Comment trouver une solution à l'aide de l'algorithme d'Euclide
• Partie 4 sur 4: Trouvez d'autres solutions infinies

Pour résoudre une équation diophantienne linéaire, vous devez trouver les valeurs des variables "x" et "y", qui sont des nombres entiers. Une solution entière est plus complexe que d'habitude et nécessite un ensemble spécifique d'actions. Tout d'abord, vous devez calculer le plus grand diviseur commun (GCD) des coefficients, puis trouver une solution. Une fois que vous avez trouvé une solution entière à une équation linéaire, vous pouvez utiliser un modèle simple pour trouver un nombre infini d'autres solutions.

Pas

Partie 1 sur 4: Comment écrire une équation

1. 1 Écrivez l'équation sous une forme standard. Une équation linéaire est une équation dans laquelle les exposants des variables ne dépassent pas 1. Pour résoudre une telle équation linéaire, écrivez-la d'abord sous forme standard. La forme standard d'une équation linéaire ressemble à ceci : ${ displaystyle Axe + Par = C}$, où ${ style d'affichage A, B}$ et ${ style d'affichage C}$ - des nombres entiers.
   • Si l'équation est donnée sous une forme différente, ramenez-la à une forme standard en utilisant des opérations algébriques de base. Par exemple, étant donné l'équation ${ displaystyle 23x + 4y-7x = -3y + 15}$... Donnez des termes similaires et écrivez l'équation comme ceci : ${ style d'affichage 16x + 7y = 15}$.
2. 2 Simplifiez l'équation (si possible). Lorsque vous écrivez l'équation sous forme standard, regardez les coefficients ${ style d'affichage A, B}$ et ${ style d'affichage C}$... Si ces cotes ont un PGCD, divisez les trois cotes par celui-ci. La solution d'une telle équation simplifiée sera également la solution de l'équation d'origine.
   • Par exemple, si les trois coefficients sont pairs, divisez-les par au moins 2. Par exemple :
     • ${ style d'affichage 42x + 36y = 48}$ (tous les membres sont divisibles par 2)
     • ${ style d'affichage 21x + 18y = 24}$ (maintenant tous les membres sont divisibles par 3)
     • ${ style d'affichage 7x + 6y = 8}$ (cette équation ne peut plus être simplifiée)
3. 3 Vérifiez si l'équation peut être résolue. Dans certains cas, vous pouvez immédiatement déclarer que l'équation n'a pas de solution. Si le coefficient "C" n'est pas divisible par le PGCD des coefficients "A" et "B", l'équation n'a pas de solutions.
   • Par exemple, si les deux coefficients ${ style d'affichage A}$ et ${ style d'affichage B}$ sont pairs, alors le coefficient ${ style d'affichage C}$ doit être pair. Mais si ${ style d'affichage C}$ bizarre, alors il n'y a pas de solution.
     • L'équation ${ style d'affichage 2x + 4y = 21}$ pas de solutions entières.
     • L'équation ${ style d'affichage 5x + 10y = 17}$ il n'y a pas de solutions entières puisque le côté gauche de l'équation est divisible par 5 et le côté droit ne l'est pas.

Partie 2 sur 4: Comment écrire l'algorithme d'Euclide

1. 1 Comprendre l'algorithme d'Euclide. C'est une série de divisions répétées dans lesquelles le reste précédent est utilisé comme diviseur suivant. Le dernier diviseur qui divise les nombres intégralement est le plus grand diviseur commun (GCD) des deux nombres.
   • Par exemple, trouvons le PGCD des nombres 272 et 36 en utilisant l'algorithme d'Euclide :
     • ${ style d'affichage 272 = 7 * 36 + 20}$ - Divisez le plus grand nombre (272) par le plus petit (36) et faites attention au reste (20) ;
     • ${ style d'affichage 36 = 1 * 20 + 16}$ - diviser le diviseur précédent (36) par le reste précédent (20). Notez le nouveau résidu (16) ;
     • ${ style d'affichage 20 = 1 * 16 + 4}$ - diviser le diviseur précédent (20) par le reste précédent (16). Notez le nouveau résidu (4) ;
     • ${ style d'affichage 16 = 4 * 4 + 0}$ - Diviser le diviseur précédent (16) par le reste précédent (4). Puisque le reste est 0, nous pouvons dire que 4 est le PGCD des deux nombres originaux 272 et 36.
2. 2 Appliquer l'algorithme d'Euclide aux coefficients "A" et "B". Lorsque vous écrivez l'équation linéaire sous forme standard, déterminez les coefficients "A" et "B", puis appliquez-leur l'algorithme d'Euclide pour trouver le PGCD. Par exemple, étant donné une équation linéaire ${ style d'affichage 87x-64y = 3}$.
   • Voici l'algorithme d'Euclide pour les coefficients A = 87 et B = 64 :
     • ${ style d'affichage 87 = 1 * 64 + 23}$
     • ${ displaystyle 64 = 2 * 23 + 18}$
     • ${ style d'affichage 23 = 1 * 18 + 5}$
     • ${ style d'affichage 18 = 3 * 5 + 3}$
     • ${ style d'affichage 5 = 1 * 3 + 2}$
     • ${ style d'affichage 3 = 1 * 2 + 1}$
     • ${ style d'affichage 2 = 2 * 1 + 0}$
3. 3 Trouvez le plus grand facteur commun (GCD). Puisque le dernier diviseur était 1, PGCD 87 et 64 valent 1. Ainsi, 87 et 64 sont des nombres premiers l'un par rapport à l'autre.
4. 4 Analysez le résultat. Quand vous trouvez les coefficients pgcd ${ style d'affichage A}$ et ${ style d'affichage B}$, comparez-le avec le coefficient ${ style d'affichage C}$ l'équation d'origine. Si ${ style d'affichage C}$ divisible par pgcd ${ style d'affichage A}$ et ${ style d'affichage B}$, l'équation a une solution entière ; sinon l'équation n'a pas de solutions.
   • Par exemple, l'équation ${ style d'affichage 87x-64y = 3}$ peut être résolu car 3 est divisible par 1 (pgcd = 1).
   • Par exemple, supposons que PGCD = 5. 3 n'est pas divisible par 5, donc cette équation n'a pas de solutions entières.
   • Comme indiqué ci-dessous, si une équation a une solution entière, elle a également un nombre infini d'autres solutions entières.

Partie 3 sur 4: Comment trouver une solution à l'aide de l'algorithme d'Euclide

1. 1 Numérotez les étapes de calcul du PGCD. Pour trouver la solution à une équation linéaire, vous devez utiliser l'algorithme d'Euclide comme base du processus de substitution et de simplification.
   • Commencez par numéroter les étapes de calcul du PGCD. Le processus de calcul ressemble à ceci :
     • ${ displaystyle { text {Étape 1}} : 87 = (1 * 64) +23}$
     • ${ displaystyle { text {Étape 2}} : 64 = (2 * 23) +18}$
     • ${ displaystyle { text {Étape 3}} : 23 = (1 * 18) +5}$
     • ${ displaystyle { text {Étape 4}} : 18 = (3 * 5) +3}$
     • ${ displaystyle { text {Étape 5}} : 5 = (1 * 3) +2}$
     • ${ displaystyle { text {Étape 6}} : 3 = (1 * 2) +1}$
     • ${ displaystyle { text {Étape 7}} : 2 = (2 * 1) +0}$
2. 2 Faites attention à la dernière étape, où il y a un reste. Réécrivez l'équation de cette étape pour isoler le reste.
   • Dans notre exemple, la dernière étape avec reste est l'étape 6. Le reste est 1. Réécrivez l'équation de l'étape 6 comme suit :
     • ${ style d'affichage 1 = 3- (1 * 2)}$
3. 3 Isolez le reste de l'étape précédente. Ce processus est une « montée vers le haut » étape par étape. A chaque fois, vous isolerez le reste dans l'équation de l'étape précédente.
   • Isolez le reste de l'équation à l'étape 5 :
     • ${ style d'affichage 2 = 5- (1 * 3)}$ ou alors ${ style d'affichage 2 = 5-3}$
4. 4 Remplacez et simplifiez. Notez que l'équation de l'étape 6 contient le nombre 2, et dans l'équation de l'étape 5, le nombre 2 est isolé. Ainsi, au lieu de "2" dans l'équation de l'étape 6, remplacez l'expression de l'étape 5 :
   • ${ style d'affichage 1 = 3-2}$ (équation de l'étape 6)
   • ${ style d'affichage 1 = 3- (5-3)}$ (au lieu de 2, une expression a été substituée)
   • ${ style d'affichage 1 = 3-5 + 3}$ (crochets ouverts)
   • ${ style d'affichage 1 = 2 (3) -5}$ (simplifié)
5. 5 Répétez le processus de substitution et de simplification. Répétez le processus décrit, en parcourant l'algorithme euclidien dans l'ordre inverse. À chaque fois, vous réécrirez l'équation de l'étape précédente et la connecterez à la dernière équation que vous obtenez.
   • La dernière étape que nous avons examinée était l'étape 5. Passez donc à l'étape 4 et isolez le reste de l'équation pour cette étape :
     • ${ style d'affichage 3 = 18- (3 * 5)}$
   • Remplacez cette expression par "3" dans la dernière équation :
     • ${ style d'affichage 1 = 2 (18-3 * 5) -5}$
     • ${ style d'affichage 1 = 2 (18) -6 (5) -5}$
     • ${ style d'affichage 1 = 2 (18) -7 (5)}$
6. 6 Poursuivez le processus de substitution et de simplification. Ce processus sera répété jusqu'à ce que vous atteigniez l'étape initiale de l'algorithme d'Euclide. Le but du processus est d'écrire l'équation avec les coefficients 87 et 64 de l'équation originale à résoudre. Dans notre exemple :
   • ${ style d'affichage 1 = 2 (18) -7 (5)}$
   • ${ style d'affichage 1 = 2 (18) -7 (23-18)}$ (a remplacé l'expression de l'étape 3)
     • ${ style d'affichage 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ style d'affichage 1 = 9 (18) -7 (23)}$
   • ${ style d'affichage 1 = 9 (64-2 * 23) -7 (23)}$ (a remplacé l'expression de l'étape 2)
     • ${ style d'affichage 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ style d'affichage 1 = 9 (64) -25 (23)}$
   • ${ style d'affichage 1 = 9 (64) -25 (87-64)}$ (a remplacé l'expression de l'étape 1)
     • ${ style d'affichage 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ style d'affichage 1 = 34 (64) -25 (87)}$
7. 7 Réécrivez l'équation résultante conformément aux coefficients d'origine. Lorsque vous revenez à la première étape de l'algorithme d'Euclide, vous verrez que l'équation résultante contient deux coefficients de l'équation d'origine. Réécrivez l'équation de sorte que l'ordre de ses termes corresponde aux coefficients de l'équation d'origine.
   • Dans notre exemple, l'équation originale ${ style d'affichage 87x-64y = 3}$... Par conséquent, réécrivez l'équation résultante de sorte que les coefficients soient alignés.Portez une attention particulière au coefficient "64". Dans l'équation d'origine, ce coefficient est négatif, et dans l'algorithme d'Euclide, il est positif. Par conséquent, le facteur 34 doit être rendu négatif. L'équation finale s'écrira ainsi :
     • ${ style d'affichage 87 (-25) -64 (-34) = 1}$
8. 8 Appliquez le multiplicateur approprié pour trouver une solution. Notez que dans notre exemple, PGCD = 1, donc l'équation finale est 1. Mais l'équation d'origine (87x-64y) est 3. Par conséquent, tous les termes de l'équation finale doivent être multipliés par 3 pour obtenir la solution :
   • ${ displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ style d'affichage 87 (-75) -64 (-102) = 3}$
9. 9 Écrivez la solution entière de l'équation. Les nombres qui sont multipliés par les coefficients de l'équation d'origine sont les solutions de cette équation.
   • Dans notre exemple, écrivez la solution sous la forme d'une paire de coordonnées : ${ style d'affichage (x, y) = (- 75, -102)}$.

Partie 4 sur 4: Trouvez d'autres solutions infinies

1. 1 Comprenez qu'il existe une infinité de solutions. Si une équation linéaire a une solution entière, alors elle doit avoir une infinité de solutions entières. Voici une preuve rapide (sous forme algébrique) :
   • ${ displaystyle Axe + Par = C}$
   • ${ style d'affichage A (x + B) + B (y-A) = C}$ (si vous ajoutez "B" à "x" et soustrayez "A" de "y", la valeur de l'équation d'origine ne changera pas)
2. 2 Enregistrez les valeurs x et y d'origine. Le modèle de calcul des prochaines solutions (infinies) commence par la seule solution que vous avez déjà trouvée.
   • Dans notre exemple, la solution est une paire de coordonnées ${ style d'affichage (x, y) = (- 75, -102)}$.
3. 3 Ajoutez le facteur "B" à la valeur "x". Faites ceci pour trouver la nouvelle valeur x.
   • Dans notre exemple, x = -75, et B = -64 :
     • ${ style d'affichage x = -75 + (- 64) = - 139}$
   • Ainsi, la nouvelle valeur "x": x = -139.
4. 4 Soustraire le facteur "A" de la valeur "y". Pour que la valeur de l'équation d'origine ne change pas, lorsque vous ajoutez un nombre à "x", vous devez soustraire un autre nombre de "y".
   • Dans notre exemple, y = -102, et A = 87 :
     • ${ style d'affichage y = -102-87 = -189}$
   • Ainsi, la nouvelle valeur pour "y": y = -189.
   • La nouvelle paire de coordonnées s'écrira comme ceci : ${ style d'affichage (x, y) = (- 139, -189)}$.
5. 5 Vérifiez la solution. Pour vérifier que la nouvelle paire de coordonnées est une solution à l'équation d'origine, branchez les valeurs dans l'équation.
   • ${ style d'affichage 87x-64y = 3}$
   • ${ style d'affichage 87 (-139) -64 (-189) = 3}$
   • ${ style d'affichage 3 = 3}$
   • Puisque l'égalité est respectée, la décision est correcte.
6. 6 Écrivez des expressions pour trouver de nombreuses solutions. Les valeurs "x" seront égales à la solution d'origine plus tout multiple du facteur "B". Cela peut s'écrire sous la forme de l'expression suivante :
   • x (k) = x + k (B), où "x (k)" est l'ensemble des valeurs "x" et "x" est la (première) valeur d'origine de "x" que vous avez trouvée.
     • Dans notre exemple :
     • ${ displaystyle x (k) = - 75-64k}$
   • y (k) = y-k (A), où y (k) est l'ensemble des valeurs y et y est la (première) valeur y originale que vous avez trouvée.
     • Dans notre exemple :
     • ${ displaystyle y (k) = - 102-87k}$