Comment transposer une matrice

Contenu

Pas
Partie 1 sur 3: Transposer la matrice
Partie 2 sur 3: Propriétés de transposition
Partie 3 sur 3: Matrice conjuguée hermitienne avec éléments complexes
Conseils

Si vous apprenez à transposer des matrices, vous aurez une meilleure compréhension de leur structure. Vous connaissez peut-être déjà les matrices carrées et leur symétrie pour vous aider à maîtriser la transposition. Entre autres choses, la transposition aide à transformer les vecteurs sous forme matricielle et à trouver des produits vectoriels. Lorsque vous travaillez avec des matrices complexes, les matrices conjuguées hermitiennes (conjuguées-transposées) peuvent vous aider à résoudre divers problèmes.

Pas

Partie 1 sur 3: Transposer la matrice

1 Prenez n'importe quelle matrice. N'importe quelle matrice peut être transposée, quel que soit le nombre de lignes et de colonnes. Le plus souvent, il est nécessaire de transposer des matrices carrées qui ont le même nombre de lignes et de colonnes, donc pour plus de simplicité, considérons la matrice suivante comme exemple :
- la matrice UNE =
  1  2  3
  4  5  6
  7  8  9
2 Imaginez la première ligne d'une matrice directe comme la première colonne de la matrice transposée. Écrivez simplement la première ligne sous forme de colonne :
- matrice transposée = A
- première colonne de la matrice A :
  1
  2
  3
3 Faites de même pour le reste des lignes. La deuxième ligne de la matrice d'origine deviendra la deuxième colonne de la matrice transposée. Traduire toutes les lignes en colonnes :
- UNE =
  1  4  7
  2  5  8
  3  6  9
4 Essayez de transposer une matrice non carrée. Toute matrice rectangulaire peut être transposée de la même manière. Écrivez simplement la première ligne comme première colonne, la deuxième ligne comme deuxième colonne, et ainsi de suite. Dans l'exemple ci-dessous, chaque ligne de la matrice d'origine est marquée de sa propre couleur pour mieux comprendre comment elle est transformée lors de la transposition :
- la matrice Z =
  4 7 2 1
  3 9 8 6
- la matrice Z =
  4  3
  7  9
  2  8
  1  6
5 Exprimons la transposition sous la forme d'une notation mathématique. Bien que l'idée de transposition soit très simple, il est préférable de l'écrire sous la forme d'une formule stricte. La notation matricielle ne nécessite aucun terme particulier :
- Supposons une matrice B constituée de m X m éléments (m lignes et n colonnes), alors la matrice transposée B est un ensemble de m X m éléments (n lignes et m colonnes).
- Pour chaque élément b_xy (ligne X et colonne oui) de la matrice B dans la matrice B il existe un élément équivalent b_yx (ligne oui et colonne X).

Partie 2 sur 3: Propriétés de transposition

1 (M = M. Après double transposition, la matrice originale est obtenue. C'est assez évident, car lorsque vous retransposez, vous modifiez à nouveau les lignes et les colonnes, ce qui donne la matrice d'origine.
2 Reflétez la matrice autour de la diagonale principale. Les matrices carrées peuvent être « retournées » par rapport à la diagonale principale. De plus, les éléments le long de la diagonale principale (d'un₁₁ au coin inférieur droit de la matrice) restent en place, et le reste des éléments se déplace de l'autre côté de cette diagonale et reste à la même distance de celle-ci.
- Si vous avez du mal à imaginer cette méthode, prenez un morceau de papier et dessinez une matrice 4x4. Réorganisez ensuite ses éléments latéraux par rapport à la diagonale principale. En même temps, tracez les éléments a₁₄ et un₄₁... Une fois transposés, ils doivent être intervertis comme les autres paires d'éléments latéraux.
3 Transposer la matrice symétrique. Les éléments d'une telle matrice sont symétriques par rapport à la diagonale principale. Si vous effectuez l'opération ci-dessus et "retournez" la matrice symétrique, elle ne changera pas. Tous les éléments seront remplacés par des éléments similaires. En fait, c'est la méthode standard pour déterminer si une matrice donnée est symétrique. Si l'égalité A = A est vérifiée, alors la matrice A est symétrique.

Partie 3 sur 3: Matrice conjuguée hermitienne avec éléments complexes

1 Considérons une matrice complexe. Les éléments d'une matrice complexe sont composés de parties réelles et imaginaires. Une telle matrice peut également être transposée, bien que dans la plupart des applications pratiques, des matrices conjuguées transposées ou conjuguées hermitiennes soient utilisées.
- Soit une matrice C =
  2+je 3-2je
  0+je 5+0je
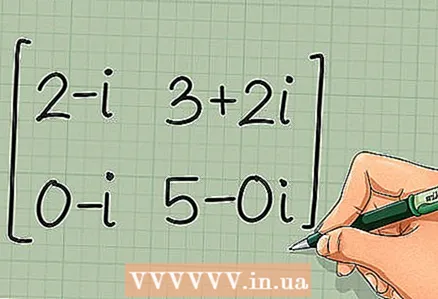2 Remplacez les éléments par des nombres conjugués complexes. Dans l'opération de conjugaison complexe, la partie réelle reste la même et la partie imaginaire change de signe en l'opposé. Faisons cela avec les quatre éléments de la matrice.
- trouver la matrice conjuguée complexe C * =
  2-je 3+2je
  0-je 5-0je
3 Nous transposons la matrice résultante. Prenez la matrice conjuguée complexe trouvée et transposez-la simplement. En conséquence, nous obtenons une matrice conjuguée-transposée (Hermitienne-conjuguée).
- la matrice conjuguée-transposée C =
  2-je 0-je
  3+2je 5-0je

Conseils

Dans cet article, la matrice transposée relative à la matrice A est notée A. Il existe également la notation A' ou Ã.
Dans cet article, la matrice hermitienne conjuguée par rapport à la matrice A est notée A, qui est une notation courante en algèbre linéaire. En mécanique quantique, la notation A est souvent utilisée.Parfois, une matrice conjuguée hermitienne s'écrit sous la forme A*, mais il vaut mieux éviter cette notation, car elle sert aussi à écrire une matrice conjuguée complexe.