Contenu

• Avancer d'un pas
• Méthode 1 sur 3: Utilisation des formules de rayon
• Méthode 2 sur 3: définir les concepts clés
• Méthode 3 sur 3: Recherche du rayon comme distance entre deux points
• Conseils

Le rayon d'une sphère (abrégé en variable r ou alors R.) est la distance entre le centre exact de la sphère et un point sur la surface de cette sphère. Comme pour les cercles, le rayon d'une sphère est souvent une métrique essentielle pour calculer le diamètre, la circonférence, l'aire et le volume d'une sphère. Cependant, vous pouvez également travailler à rebours à partir du diamètre, de la circonférence, etc. pour trouver le rayon de la sphère. Utilisez la formule adaptée aux données dont vous disposez.

Avancer d'un pas

Méthode 1 sur 3: Utilisation des formules de rayon

1. Déterminez le rayon si vous connaissez le diamètre. Le rayon est un demi-diamètre, vous utilisez donc la formule r = D / 2. Ceci est identique à la méthode de calcul du rayon d'un cercle où le diamètre est donné.
   • Si vous avez une sphère d'un diamètre de 16 cm, vous calculez le rayon avec 16/2 = 8 cm. Si le diamètre est de 42, alors le rayon est 21.
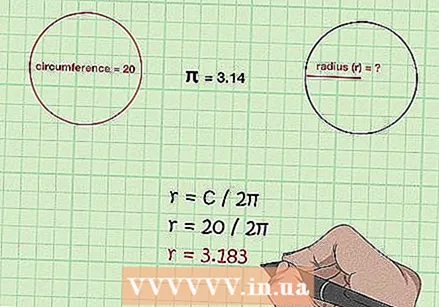2. Déterminez le rayon si vous connaissez la circonférence. Utilisez la formule C / 2π. Puisque la circonférence est égale à πD, qui à son tour est égale à 2πr, calculez le rayon en divisant la circonférence par 2π.
   • Si vous avez une sphère de 20 m de circonférence, vous trouverez le rayon avec 20 / 2π = 3,183 m.
   • Vous pouvez utiliser la même formule pour convertir entre le rayon et la circonférence d'un cercle.
3. Calculez le rayon si vous connaissez le volume de la sphère. Utilisez la formule ((V / π) (3/4)). Le volume d'une sphère est dérivé de l'équation V = (4/3) πr. En résolvant l'équation pour r, vous obtenez ((V / π) (3/4)) = r, il devient donc clair que le rayon d'une sphère ou est égal au volume divisé par π, multiplié par 3/4, à la puissance 1/3 (ou racine cubique).
   • Si vous avez une sphère d'un volume de 100 cm, vous obtenez le rayon comme suit:
     • ((V / π) (3/4)) = r
     • ((100 / π) (3/4)) = r
     • ((31,83) (3/4)) = r
     • (23,87) = r
     • 2,88 = r
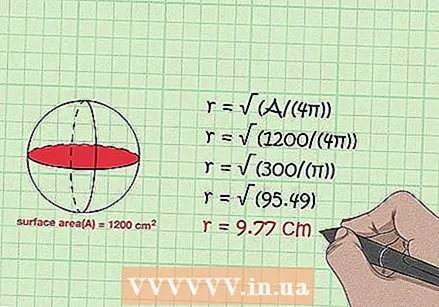4. Déterminez le rayon de la surface. Utilisez la formule r = √ (A / (4π)). Vous calculez l'aire d'une sphère avec l'équation A = 4πr. La résolution de l'équation pour r donne √ (A / (4π)) = r, ce qui signifie que le rayon d'une sphère est égal à la racine carrée de son aire divisée par 4π. Vous pouvez également mettre (A / (4π)) à 1/2 pour le même résultat.
   • Si vous avez une sphère d'une superficie de 1200 cm, vous calculez le rayon comme suit:
     • √ (A / (4π)) = r
     • √ (1200 / (4π)) = r
     • √ (300 / (π)) = r
     • √ (95,49) = r
     • 9,77 cm = r

Méthode 2 sur 3: définir les concepts clés

1. Connaître les dimensions de base d'une sphère. Le rayon (r) est la distance entre le centre exact de la sphère et n'importe quel point de la surface de la sphère. En général, vous pouvez trouver le rayon d'une sphère si vous connaissez son diamètre, sa circonférence, son volume ou sa surface.
   • Diamètre (D): la longueur de la ligne passant par le centre d'une sphère & ndash; double le rayon. Le diamètre est la longueur d'une ligne passant par le centre de la sphère, d'un point à l'extérieur de la sphère à un point correspondant directement en face de celle-ci. En d'autres termes, la plus grande distance possible entre deux points de la sphère.
   • Circonférence (C): la distance unidimensionnelle autour de la sphère à son point le plus large. En d'autres termes, la circonférence de la section transversale circulaire d'une sphère, dont le plan passe par le centre de la sphère.
   • Volume (V): l'espace tridimensionnel dans la sphère. C'est «l'espace occupé par la sphère».
   • Surface (A): l'espace bidimensionnel sur la surface extérieure de la sphère. La quantité d'espace plat qui couvre l'extérieur de la sphère.
   • Pi (π): une constante exprimant le rapport de la circonférence du cercle au diamètre du cercle. Les 10 premiers chiffres de Pi sont toujours 3,141592653, bien que cela soit généralement arrondi à 3,14.
2. Utilisez différentes mesures pour déterminer le rayon. Vous pouvez utiliser le diamètre, la circonférence, le volume et la surface pour calculer le rayon d'une sphère. Si vous connaissez la longueur du rayon, vous pouvez calculer l'un de ces nombres. Ainsi, pour trouver le rayon, vous pouvez inverser les formules de calcul de ces pièces. Apprenez les formules de rayon pour calculer le diamètre, la circonférence, la surface et le volume.
   • D = 2r. Comme pour les cercles, le diamètre d'une sphère est le double du rayon.
   • C = πD ou 2πr. Comme pour les cercles, la circonférence d'une sphère est égale à π fois son diamètre. Puisque le diamètre est deux fois le rayon, on peut aussi dire que la circonférence est deux fois le rayon fois π.
   • V = (4/3) πr. Le volume d'une sphère est le rayon de la puissance cubique (r x r x r), multiplié par π, multiplié par 4/3.
   • A = 4πr. L'aire d'une sphère est le rayon à la puissance de deux (rxr) fois π, fois 4. Puisque la circonférence d'un cercle est πr, on peut aussi dire que l'aire d'une sphère est égale à quatre fois l'aire d'un cercle, telle que formée par sa circonférence.

Méthode 3 sur 3: Recherche du rayon comme distance entre deux points

1. Trouvez les coordonnées (x, y, z) du centre de la sphère. Une façon de penser au rayon d'une sphère est la distance entre le centre de la sphère et n'importe quel point de sa surface. Dans la mesure où cela est vrai, vous pouvez utiliser les coordonnées du centre et un point sur la surface de la sphère pour déterminer le rayon de la sphère en calculant la distance entre les deux points à l'aide d'une variation de la formule de distance standard. Pour commencer, trouvez les coordonnées du centre de la sphère. Notez qu'une sphère est tridimensionnelle, ce sera un point (x, y, z) au lieu d'un point (x, y).
   • C'est plus facile à comprendre avec un exemple. Supposons qu'une sphère soit donnée avec comme centre (-1, 4, 12). Dans les prochaines étapes, nous allons utiliser ce point pour déterminer le rayon.
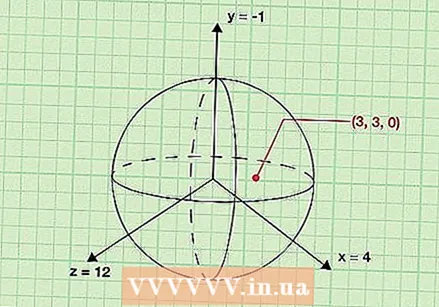2. Trouvez les coordonnées d'un point sur la surface de la sphère. Ensuite, vous devez déterminer les coordonnées (x, y, z) d'un point sur la surface de la sphère. C'est possible chaque point sur la surface de la sphère. Étant donné que, par définition, tous les points de la surface d'une sphère sont équidistants du centre, vous pouvez utiliser n'importe quel point pour déterminer le rayon.
   • Dans le contexte de notre exercice d'exemple, nous faisons valoir que le point (3, 3, 0) à la surface de la sphère. En calculant la distance entre ce point et le centre, nous pouvons trouver le rayon.
3. Déterminez le rayon avec la formule d = √ ((x₂ - X₁) + (y₂ - y₁) + (z₂ - z₁)). Maintenant que vous connaissez le centre de la sphère et un point sur la surface de la sphère, vous pouvez connaître le rayon en calculant la distance qui les sépare. Utilisez la formule de distance tridimensionnelle d = √ ((x₂ - X₁) + (y₂ - y₁) + (z₂ - z₁)), où d est la distance, (x₁, y₁, z₁) représente les coordonnées du centre, et (x₂, y₂, z₂) représente les coordonnées du point sur la surface pour déterminer la distance entre les deux points.
   • Dans notre exemple, nous substituons (4, -1, 12) à (x₁, y₁, z₁) et (3, 3, 0) pour (x₂, y₂, z₂), en résolvant ceci comme suit:
     • d = √ ((x₂ - X₁) + (y₂ - y₁) + (z₂ - z₁))
     • d = √ ((3 - 4) + (3 - -1) + (0 - 12))
     • d = √ ((- 1) + (4) + (-12))
     • d = √ (1 + 16 + 144)
     • d = √ (161)
     • d = 12,69. C'est le rayon de notre sphère.
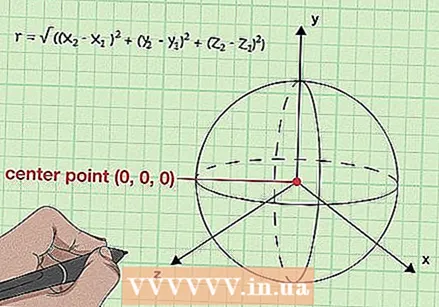4. En général, sachez que r = √ ((x₂ - X₁) + (y₂ - y₁) + (z₂ - z₁)). Dans une sphère, chaque point de la surface a la même distance par rapport au centre de la sphère. En prenant la formule de distance tridimensionnelle ci-dessus et en remplaçant la variable «d» par la variable «r» du rayon, nous obtenons une équation qui nous permet de trouver le rayon à tout point central donné (x₁, y₁, z₁) et tout point correspondant sur la surface (x₂, y₂, z₂).
   • En mettant au carré les deux côtés de cette équation, nous obtenons: r = (x₂ - X₁) + (y₂ - y₁) + (z₂ - z₁). Remarque: C'est essentiellement la même chose que l'équation standard pour une sphère (r = x + y + z), en supposant que le centre est égal à (0,0,0).

Conseils

• L'ordre des opérations est important. Si vous n'êtes pas sûr du fonctionnement des règles de calcul et que votre calculatrice prend en charge les parenthèses, assurez-vous de les utiliser.
• Cet article a été créé car ce sujet était très demandé. Cependant, si vous essayez de comprendre la géométrie spatiale pour la première fois, il est probablement préférable de commencer par l'autre côté: calculer les propriétés d'une sphère lorsque le rayon est donné.
• Pi ou π est une lettre grecque qui indique le rapport du diamètre d'un cercle à sa circonférence. C'est un nombre irrationnel et ne peut pas être écrit comme un rapport de nombres réels. Il existe de nombreuses approximations et 333/106 renvoie pi à quatre décimales. Aujourd'hui, la plupart des gens se souviennent de l'approximation 3,14 qui est généralement assez précise pour les besoins quotidiens.